Bienvenue dans cet article consacré aux exercices sur les calculs commerciaux et plus précisément sur comment calculer une remise en pourcentage. Vous trouverez ici pas moins de 11 exercices corrigés détaillés de gestion sur les calculs commerciaux pour la Gestion Opérationnelle.
A la fin de cet article, vous saurez comment calculer une remise en pourcentage dans les calculs commerciaux sans aucun soucis.
Sommaire
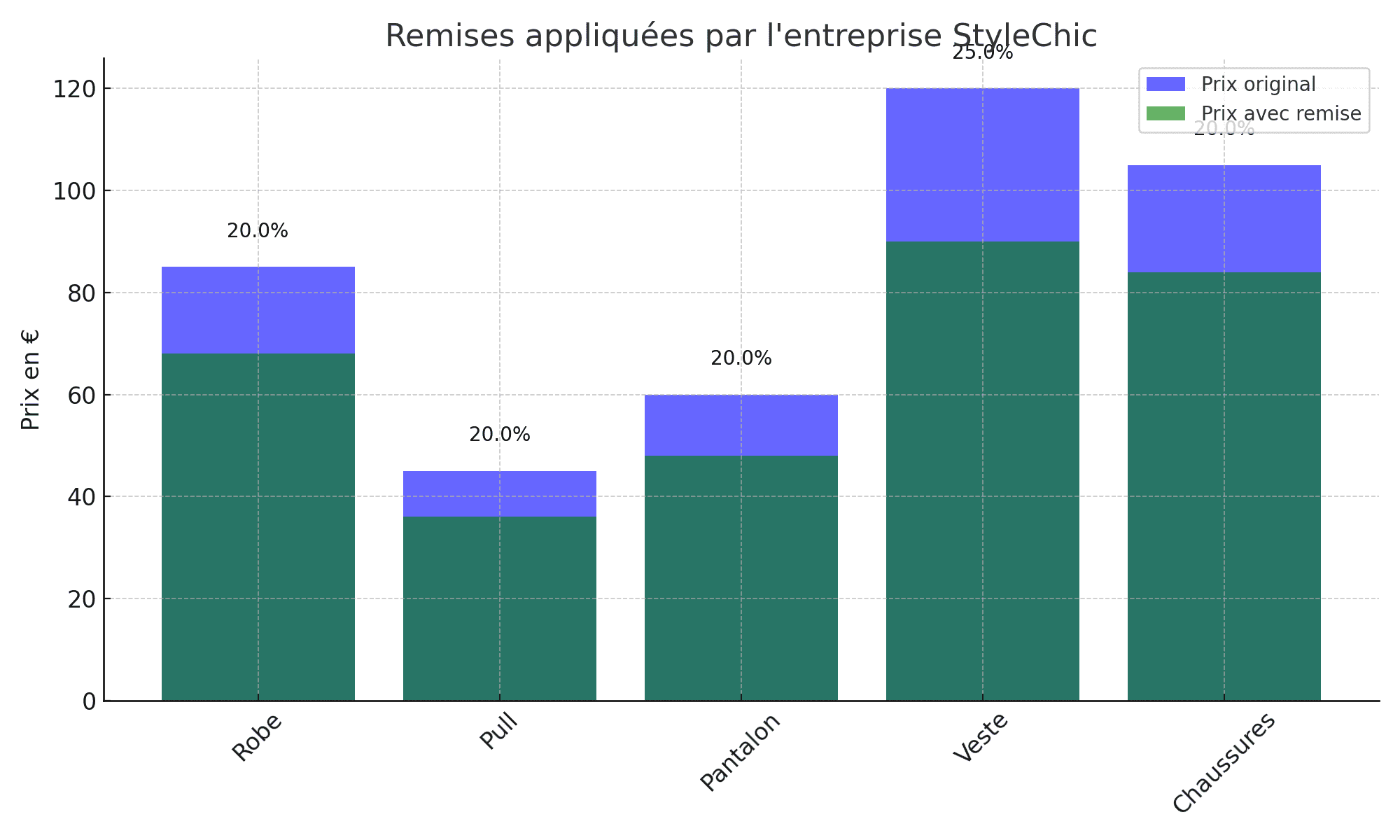
Application StyleChic
Énoncé :
Dans l’entreprise de prêt-à-porter StyleChic, le gérant a décidé d’octroyer des remises sur certains articles pour attirer plus de clients et accroître le volume de ses ventes. Vous êtes chargé de calculer le taux de ces remises. Voici quelques exemples de remises accordées par l’entreprise StyleChic :
1. Pour une robe dont le prix original est de 85 €, une remise de 17 € a été appliquée.
2. Un pull vendu initialement à 45 € a bénéficié d’une remise de 9 €.
3. Un pantalon de 60 € a été réduit de 12 €.
4. Une veste à 120 € a subi une remise de 30 €.
5. Des chaussures de 105 € ont été remisées de 21 €.
Travail à faire :
1. Quel est le taux de remise appliqué à la robe ?
2. Quel est le taux de la remise accordée sur le pull ?
3. Quel est le taux de remise octroyé sur le pantalon ?
4. Quel est le taux de la remise effectuée sur la veste ?
5. Quel est le taux de remise appliqué sur les chaussures ?
Proposition de correction :
La formule pour calculer le taux de remise est la suivante : Taux de remise = (Montant de la remise / Prix avant remise) x 100.
1. La remise appliquée à la robe est de : (17€ / 85€) x 100 = 20%
2. La remise accordée sur le pull est de : (9€ / 45€) x 100 = 20%
3. Le taux de remise octroyé sur le pantalon est : (12€ / 60€) x 100 = 20%
4. Le taux de la remise effectuée sur la veste est : (30€ / 120€) x 100 = 25%
5. Le taux de remise appliqué sur les chaussures est : (21€ / 105€) x 100 = 20%
Récapitulatif des Formules Utilisées :
– Taux de remise = (Montant de la remise / Prix avant remise) x 100
Application Les mots d’or
Énoncé :
La librairie Les mots d’or propose une variété de livres. Afin d’encourager la lecture, le gestionnaire décide d’organiser une vente avec des remises sur certains livres.
Les informations suivantes sont disponibles :
1. Le livre “Les aventures du héros” coûte 25 € sans remise. Pendant la vente, son prix est réduit à 20 €.
2. Le livre “Passage vers l’inconnu” coûte 15 € sans remise. Pendant la vente, son prix est réduit à 13,50 €.
3. Le livre “Au coeur de la science” coûte 30 € sans remise. Pendant la vente, son prix est réduit à 27 €.
4. Le livre “Mystères de l’histoire” coûte 20 € sans remise. Pendant la vente, son prix est réduit à 18 €.
5. Le livre “Récits fantastiques” coûte 10 € sans remise. Pendant la vente, son prix est réduit à 9 €.
Travail à faire :
1. Quel est le pourcentage de remise appliqué sur le livre “Les aventures du héros” ?
2. Quel est le pourcentage de remise appliqué sur le livre “Passage vers l’inconnu” ?
3. Quel est le pourcentage de remise appliqué sur le livre “Au coeur de la science” ?
4. Quel est le pourcentage de remise appliqué sur le livre “Mystères de l’histoire” ?
5. Quel est le pourcentage de remise appliqué sur le livre “Récits fantastiques” ?
Proposition de correction :
La formule pour calculer une remise en pourcentage est la suivante :
Pourcentage de remise = ((Prix initial – Prix après remise) / Prix initial) x 100
1. Pourcentage de remise sur le livre “Les aventures du héros” = ((25 € – 20 €) / 25 €) x 100 = 20 %.
2. Pourcentage de remise sur le livre “Passage vers l’inconnu” = ((15 € – 13,50 €) / 15 €) x 100 = 10 %.
3. Pourcentage de remise sur le livre “Au coeur de la science” = ((30 € – 27 €) / 30 €) x 100 = 10 %.
4. Pourcentage de remise sur le livre “Mystères de l’histoire” = ((20 € – 18 €) / 20 €) x 100 = 10 %.
5. Pourcentage de remise sur le livre “Récits fantastiques” = ((10 € – 9 €) / 10 €) x 100 = 10 %.
Récapitulatif des Formules Utilisées :
Pourcentage de remise = ((Prix initial – Prix après remise) / Prix initial) x 100
Application Maison Cosy
Énoncé :
Sarah est la gestionnaire financière de l’entreprise Maison Cosy. Cette boutique, spécialisée dans la vente de meubles et décoration intérieure, propose souvent des promotions à ses clients.
Un jour, le gérant décide de faire une vente flash sur certains articles, notamment sur un canapé qui coûte à l’origine 750 €. Sarah doit alors calculer les réductions pour plusieurs scénarios de remises pour cette vente flash.
Travail à faire :
1. Calculez le prix du canapé si une remise de 10% est appliquée.
2. Calculez le prix du canapé si une remise de 25% est appliquée.
3. Calculez le prix du canapé si une remise de 50% est appliquée.
4. Calculez le prix du canapé si une remise de 75% est appliquée.
5. Quel serait le pourcentage de remise si le canapé est vendu à 550 € ?
Proposition de correction :
1. Prix après remise de 10% = Prix initial – (Prix initial x 10%)
Prix après remise = 750 € – (750 € x 10 / 100)
Prix après remise = 750 € – 75 € = 675 €.
2. Prix après remise de 25% = Prix initial – (Prix initial x 25%)
Prix après remise = 750 € – (750 € x 25 / 100)
Prix après remise = 750 € – 187,50 € = 562,50 €.
3. Prix après remise de 50% = Prix initial – (Prix initial x 50%)
Prix après remise = 750 € – (750 € x 50 / 100)
Prix après remise = 750 € – 375 € = 375 €.
4. Prix après remise de 75% = Prix initial – (Prix initial x 75%)
Prix après remise = 750 € – (750 € x 75 / 100)
Prix après remise = 750 € – 562,50 € = 187,50 €.
5. Pourcentage de remise = ((Prix initial – Prix de vente) / Prix initial) x 100
Pourcentage de remise = ((750 € – 550 €) / 750 €) x 100
Pourcentage de remise = (200 € / 750 €) x 100 = 26,67% (arrondi à deux chiffres après la virgule)
Récapitulatif des Formules Utilisées :
1. Calcul du montant de la remise : Montant initial x taux de remise (%)
2. Calcul du prix après remise : Montant initial – Montant de la remise
3. Calcul du pourcentage de remise : ((Prix initial – Prix de vente) / Prix initial) x 100.
Application Fashion Retail
Énoncé :
L’entreprise Fashion Retail vend une robe à ses clients. Le prix de vente initial de la robe est de 80 €. Fashion Retail décide d’offrir une remise sur ce produit.
Travail à faire :
1/ Si le prix est réduit de 15 €, quelle est le pourcentage de la remise ?
2/ Si le prix est réduit de 20 %, quel est le nouveau prix de la robe ?
3/ Si le prix est réduit de 50 %, quel est le nouveau prix de la robe ?
4/ Si le prix est réduit à 40 €, quel est le pourcentage de la remise ?
5/ Si le prix est réduit de 25 %, quel est le nouveau prix de la robe ?
Proposition de correction :
1/ Le pourcentage de remise se calcule comme suit : (Montant de la remise ÷ Prix initial ) x 100
Soit, (15 ÷ 80) x 100 = 18,75%
Donc, le pourcentage de la remise est donc de18,75%.
2/ Pour trouver le nouveau prix après une remise de 20 %, on se sert de la formule : Prix initial x (1 – Taux de remise)
Soit, 80 x (1 – 20/100) = 64 €
Donc, le nouveau prix de la robe après une remise de 20% serait donc de 64 €.
3/ Similairement, pour une remise de 50 %: 80 x (1 – 50/100) = 40 €
Donc, le nouveau prix de la robe après une remise de 50 % serait de 40 €.
4/ Pour calculer le pourcentage de remise lorsque le nouveau prix est connu, on utilise la formule : ((Prix initial – Nouveau Prix) ÷ Prix initial ) x 100
Soit, ((80 – 40) ÷ 80) x 100 = 50%
Donc, le pourcentage de la remise lorsque le prix est réduit à 40 € est de 50%.
5/ Enfin, pour une remise de 25 %: 80 x (1 – 25 /100) = 60 €
Donc, le nouveau prix de la robe après une remise de 25 % serait de 60 €.
Récapitulatif des Formules Utilisées :
– Pourcentage de remise : (Montant de la remise ÷ Prix initial ) x 100
– Nouveau prix après remise : Prix initial x (1 – Taux de remise)
– Pourcentage de remise lorsque le nouveau prix est connu : ((Prix initial – Nouveau Prix) ÷ Prix initial ) x 100
Application Hautain DeBordeaux
Énoncé :
Votre ami, Hautain DeBordeaux, est le propriétaire d’une boutique de vin à la campagne. Il veut organiser une promotion sur l’une de ses bouteilles Baux Rouges, un vin excellent qu’il vend habituellement à 60€ la bouteille. Afin d’augmenter ses ventes, il planifie de proposer une réduction de 10€ sur chaque bouteille vendue pendant une semaine. Cependant, il n’a pas pris le temps de calculer en pourcentage cette réduction.
Votre ami vous demande votre aide pour réaliser ces calculs, en vous posant les questions suivantes :
Travail à faire :
1. Quel est le montant initial de la bouteille de vin avant réduction ?
2. Quelle est la valeur de la réduction en euros ?
3. Calculer le prix du vin après la réduction.
4. Quel est le pourcentage de la réduction offerte par Hautain ?
5. Si j’ai 105 bouteilles en stock, combien vais-je perdre en total si je les vends toutes avec la réduction ?
Proposition de correction :
1. Le montant initial de la bouteille de vin avant réduction est de 60€.
2. La valeur de la réduction en euros est de 10€.
3. Le prix du vin après la réduction est calculé en soustrayant la réduction du prix initial. Donc 60€ – 10€ = 50€.
4. Le pourcentage de la réduction est calculé en divisant la réduction en euros par le prix initial, puis en multipliant par 100. Donc (10€ / 60€) x 100 = 16,67%. Hautain offre donc une réduction d’environ 17%.
5. Si Hautain a 105 bouteilles en stock, le montant total de la réduction sera de 105 x 10€ = 1050€. Hautain perdra donc 1050€ en total s’il vend toutes les bouteilles avec la réduction.
Récapitulatif des Formules Utilisées :
1. Prix après réduction = Prix initial – Réduction en euros
2. Pourcentage de réduction = (Réduction en euros / Prix initial) x 100
3. Montant total de perte = Nombre de bouteilles en stock x Réduction en euros
Application EuroDiscount
Énoncé :
L’entreprise EuroDiscount, spécialisée dans la vente de produits électroménagers, propose à ses clients diverses opérations promotionnelles, notamment des remises en pourcentage. Cette année, l’entreprise veut analyser et évaluer l’impact de ces remises sur ses marges et ses prix.
- Le lave-linge Aquamax, qui se vend habituellement à 600 € HT, a été proposé avec une remise de 15% pendant une période de vente.
- Le réfrigérateur FrigoPro, dont le prix habituel est de 1000 € HT, a bénéficié d’une remise de 20%
- Le mixeur MaxMix, vendu à 75 € HT, est proposé avec une remise de 25%
Voici les coûts d’achat HT des produits : Aquamax (350 €), FrigoPro (700 €), MaxMix (30 €).
Travail à faire :
1. Calculez le montant de la remise pour chaque produit et le nouveau prix de vente HT en conséquence.
2. Calculez le taux de marge avant et après la remise pour chaque produit.
3. Évaluez l’impact de ces remises sur la marge globale de l’entreprise.
4. Quel produit présente la plus grande baisse du taux de marge à la suite de la remise ?
5. L’entreprise peut-elle se permettre de proposer de telles promotions régulièrement ou devrait-elle réévaluer sa stratégie de remise ?
Proposition de correction :
1.
– Pour l’Aquamax : Remise = 15/100 x 600 = 90 €. Nouveau prix HT = 600 – 90 = 510 €.
– Pour le FrigoPro : Remise = 20/100 x 1000 = 200 €. Nouveau prix HT = 1000 – 200 = 800 €.
– Pour le MaxMix : Remise = 25/100 x 75 = 18.75 €. Nouveau prix HT = 75 – 18.75 = 56.25 €.
2.
– Pour l’Aquamax :
– Taux de marge avant remise = ((600 – 350) / 350) x 100 = 71.43%.
– Taux de marge après remise = ((510 – 350) / 350) x 100 = 45.71%.
– Pour le FrigoPro :
– Taux de marge avant remise = ((1000 – 700) / 700) x 100 = 42.86%.
– Taux de marge après remise = ((800 – 700) / 700) x 100 = 14.29%.
– Pour le MaxMix :
– Taux de marge avant remise = ((75 – 30) / 30) x 100 = 150%.
– Taux de marge après remise = ((56.25 – 30) / 30) x 100 = 87.5%.
3. Avec les données disponibles, nous pouvons calculer l’impact sur la marge globale en sommant les produits des marges unitaires et des quantités vendues pour chaque produit :
Marge total avant remises = (600 – 350) + (1000 – 700) + (75 – 30) = 595 €
Marge total après remises = (510 – 350) + (800 – 700) + (56.25 – 30) = 286.25 €
Impact en pourcentage sur la marge = ((595 – 286.25) / 595) x 100 = 51.9%
4. Le FrigoPro a la plus grande baisse du taux de marge (de 42.86% à 14.29%), soit une baisse de 66.67%.
5. Si l’entreprise souhaite maintenir sa rentabilité, elle doit faire preuve de prudence dans sa politique de remises. Une baisse de 51.9% du bénéfice global peut s’avérer problématique à long terme. Elle doit donc revoir sa stratégie de remises en veillant à ne pas trop impacter sa marge.
Récapitulatif des Formules Utilisées :
– Remise en € = % de remise / 100 x Prix HT initial
– Nouveau Prix HT = Prix HT initial – Remise en €
– Taux de marge = ((Prix de vente HT – Coût d’achat HT) / Coût d’achat HT) x 100
– Marge globale avant/après remises = ?(Prix de vente HT – coût d’achat HT) pour chaque produit avant/après remises
– Impact sur la marge = ((marge totale avant remises – marge totale après remises) / marge totale avant remises) x 100
– Baisse du taux de marge = ((taux de marge avant remise – taux de marge après remise) / taux de marge avant remise) x 100
Application Frisboy
Énoncé :
Un salon de coiffure incroyable, Frisboy, propose des réductions spéciales à ses clients chaque mois. Ce mois-ci, ils proposent une réduction de 20% sur leur service le plus populaire : une coupe de cheveux, qui a un prix régulier de 50 €.
Travail à faire :
1. Combien coûterait le service au client après la réduction ?
2. Combien d’euros le client économise-t-il grâce à la réduction ?
3. Si la remise avait été de 25%, combien coûterait le service ?
4. Combien d’euros le client économise-t-il si la remise est de 25% ?
5. Si le service était en vente pour 35 € après la réduction, quel était le pourcentage de la remise ?
Proposition de correction :
1. Pour trouver le coût du service après la réduction, nous utilisons la formule suivante : Prix de base – (Prix de base x pourcentage de réduction). Donc, 50 € – (50 € x 20/100) = 50 € – 10 € = 40 €. Le service coûterait donc 40 € au client après la remise.
2. Le client économise le montant de la remise, qui est de 50 € x 20/100 = 10 €. Le client économise donc 10 €.
3. Si la remise était de 25%, le service coûterait : 50 € – (50 € x 25/100) = 50 € – 12,5 € = 37,5 €. Donc, si la remise était de 25%, le service coûterait 37,5 €.
4. Avec une remise de 25%, le client économiserait : 50 € x 25/100 = 12,5 €. Donc, le client économise 12,5 €.
5. Si le service était en vente pour 35 € après la réduction, le pourcentage de la réduction serait : ((50 € – 35 €) / 50 €) x 100 = 15/50 x 100 = 30%. Donc, la réduction était de 30%.
Récapitulatif des Formules Utilisées :
– Pour calculer le coût après la réduction : Prix de base – (Prix de base x pourcentage de réduction)
– Pour calculer le montant de la remise : Prix de base x pourcentage de réduction
– Pour calculer le pourcentage de la remise si on connaît le prix après la remise : ((Prix de base – Prix après la remise) ÷ Prix de base) x 100
Application Fashion Chic
Énoncé :
La boutique de mode Fashion Chic propose divers vêtements tendance à ses clients tout au long de l’année. À la fin de la saison, la boutique organise une grande vente avec des rabais sur plusieurs articles.
Un pantalon en particulier initialement vendu à 60 € est maintenant offert avec une réduction de 15 %. Plus tard dans la vente, la boutique décide de proposer un rabais supplémentaire de 10 % sur le prix déjà réduit.
Travail à faire :
1. Quel est le montant de la remise pour la première réduction ?
2. Quel est le nouveau prix après la première réduction ?
3. Quel est le montant de la remise pour la deuxième réduction ?
4. Quel est le nouveau prix final après la deuxième réduction ?
5. Quelle est la valeur totale de la remise en pourcentage sur le prix initial ?
Proposition de correction :
1. Pour calculer le montant de la remise pour la première réduction, nous utilisons la formule : (Prix initial x taux de remise) ÷ 100. Donc, (60 € x 15) ÷ 100 = 9 €
2. Le nouveau prix après la première réduction peut être calculé en soustrayant la remise du prix initial : 60 € – 9 € = 51 €
3. Pour calculer le montant de la remise pour la deuxième réduction, nous utilisons la même formule sur le nouveau prix : (Prix réduit x taux de remise) ÷ 100. Donc, (51 € x 10) ÷ 100 = 5,10 €
4. Le nouveau prix final après la deuxième réduction peut être calculé en soustrayant la deuxième remise du prix réduit : 51 € – 5,10 € = 45,90 €
5. Pour trouver la valeur totale de la remise en pourcentage sur le prix initial, nous additionnons les deux taux de remise offerts : 15 % + 10 %.
Cependant, cela donne 25 % qui serait correct si le deuxième rabais avait été appliqué au prix original. En réalité, le deuxième rabais a été appliqué après le premier, donc la remise réelle est légèrement inférieure à 25 %.
Nous devons donc utiliser cette formule pour obtenir la remise totale en pourcentage : 100 x (1 – (Prix final ÷ Prix initial)). Donc, 100 x (1 – (45,90 € ÷ 60 €)) = 23,5 %
Récapitulatif des Formules Utilisées :
– Montant de la remise = (Prix initial x taux de remise) ÷ 100
– Nouveau prix après réduction = Prix initial – Montant de la remise
– Remise totale en pourcentage = 100 x (1 – (Prix final ÷ Prix initial))
Application Bijou Élégance
Énoncé :
L’entreprise Bijou Élégance spécialisée dans la conception de bijoux a décidé d’organiser une vente exceptionnelle au cours de laquelle elle octroie une remise sur certains de ses produits.
Le propriétaire, Mr. Dubois, fixe les prix de vente (PV) des produits comme suit :
– Bracelet en or : 2000 €
– Collier en diamant : 5000 €
– Montre en argent : 1500 €
Mr. Dubois a décidé d’octroyer des remises sur ses produits :
– Bracelet en or : remise de 300 €
– Collier en diamant : remise de 1000 €
– Montre en argent : remise de 200 €
Travail à faire :
1. Calculer la remise en pourcentage pour le bracelet en or.
2. Calculer la remise en pourcentage pour le collier en diamant.
3. Calculer la remise en pourcentage pour la montre en argent.
4. Quel produit a la plus grande remise en pourcentage ?
5. Quel produit a la plus petite remise en pourcentage ?
Proposition de correction :
1. Remise en pourcentage pour le bracelet en or = (Remise / PV) x 100 = (300 € / 2000 €) x 100 = 15%
2. Remise en pourcentage pour le collier en diamant = (Remise / PV) x 100 = (1000 € / 5000 €) x 100 = 20%
3. Remise en pourcentage pour la montre en argent = (Remise / PV) x 100 = (200 € / 1500 €) x 100 = 13,33%
4. Le produit qui a la plus grande remise en pourcentage est le “Collier en diamant” avec une remise de 20%.
5. Le produit qui a la plus petite remise en pourcentage est la “Montre en argent” avec une remise de 13,33%.
Récapitulatif des Formules Utilisées :
– Pour calculer la remise en pourcentage, la formule est Remise en % = (Remise / Prix de vente) x 100. On utilise cette formule pour les 3 premières questions où on calcule la remise en pourcentage pour trois différents produits.
– Pour déterminer quel produit a la plus grande ou la plus petite remise en pourcentage, il suffit de comparer les pourcentages de remise de chaque produit et d’identifier le plus élevé et le plus bas.
Application All-Star
Énoncé :
La société All-Star est un magasin de chaussures de sport très renommé dans la ville de Marseille. Elle dispose d’une large gamme de produits destinés aux sportifs de haut niveau et aux amateurs de sport.
La direction de All-Star décide de faire une remise spéciale sur l’ensemble des produits pendant la période estivale afin de booster les ventes et d’attirer de nouveaux clients.
Le prix initial de la chaussure de référence SportMax est de 120 € avant application de la remise.
Travail à faire :
1. Si la remise s’élève à 15% sur le produit SportMax, quel sera le nouveau prix après remise ?
2. Quel est le montant de la remise ?
3. Si un client achète 3 paires de SportMax après la remise, combien aurait-il payé sans remise ?
4. Quel est le pourcentage de remise si le prix d’une paire de SportMax passe de 120 € à 90 € ?
5. Si le magasin décide d’offrir un rabais supplémentaire de 10% après l’application de la première remise de 15% sur le produit SportMax, quel sera le prix de la paire de SportMax après ces deux remises ?
Proposition de correction :
1. Le nouveau prix après remise se calcule comme suit: Prix initial – (Prix initial x Ta% de remise). Dans notre cas: 120 € – (120 € x 15/100) = 102 €.
2. Le montant de la remise s’élève à: Prix initial x Taux de remise. Dans notre cas: 120 € x 15/100 = 18 €.
3. Sans remise, pour 3 paires de SportMax, le client aurait payé: Prix initial x quantité. Dans notre cas: 120 € x 3 = 360 €.
4. Le pourcentage de remise se calcule avec la formule : ((Prix initial – Prix après remise) / Prix initial) x 100. Dans notre cas : ((120 € – 90 €) / 120 €) x 100 = 25 %.
5. Pour calculer le prix après deux remises successives, on procède étape par étape. D’abord on applique la première remise de 15% qui nous donne un prix de 102 €. Ensuite, on applique la deuxième remise de 10 % sur ce nouveau prix : 102 € – (102 € x 10/100) = 91,8 €.
Récapitulatif des Formules Utilisées :
– Nouveau prix après remise : Prix initial – (Prix initial x Taux de remise)
– Montant de la remise : Prix initial x Taux de remise
– Total sans remise : Prix initial x Quantité
– Pourcentage de remise : ((Prix initial – Prix après remise) / Prix initial) x 100
– Prix après deux remises successives : (Prix initial – (Prix initial x Taux de première remise)) – ((Prix initial – (Prix initial x Taux de première remise)) x Taux de deuxième remise)
Application High Tech
Énoncé :
L’entreprise High Tech souhaite faire une promotion sur l’une de ses tablettes les plus populaires. Le prix de vente initial avant remise de la tablette est de 499 € et l’entreprise a décidé d’appliquer différents taux de remise sur le produit lors de différents moments de la promotion.
Travail à faire :
1. Quel est le nouveau prix après une remise de 15 % ?
2. L’entreprise décide ensuite de faire une deuxième remise de 10 %. Quel est alors le nouveau prix?
3. L’entreprise donne ensuite une remise de 5% sur le nouveau prix, quel est maintenant le prix final de la tablette ?
4. Combien l’entreprise a-t-elle offert en total de remise en € depuis le prix initial ?
5. Quel est le pourcentage total des remises offertes sur le prix initial ?
Proposition de correction :
1. Le nouveau prix après une remise de 15% est : 499 € – (15/100 x 499 €) = 424,15 €.
2. Le nouveau prix après une deuxième remise de 10% est : 424,15 € – (10/100 x 424,15 €)= 381,735 €.
3. Après une remise de 5% sur le nouveau prix, le prix de la tablette est : 381,735 € – (5/100 x 381,735 €)= 362,64825 €.
4. Le total des remises offertes depuis le prix initial est : 499 € – 362,64825 € = 136,35175 €.
5. Le pourcentage total des remises offertes sur le prix initial est : (136,35175 € / 499 €) x 100 = 27,32 %.
Récapitulatif des Formules Utilisées :
– Nouveau prix après remise = Prix initial – (Taux de remise / 100) x Prix initial
– Total des remises en € = Prix initial – Prix final après remises
– Pourcentage total des remises = (Total des remises en € / Prix initial) x 100