Comment calculer une augmentation en pourcentage

Bienvenue dans cet article consacré aux exercices sur les calculs commerciaux et plus précisément sur comment calculer une augmentation en pourcentage. Vous trouverez ici des questions et réponses en relation avec le sujet. Mais aussi pas moins de 9 exercices corrigés détaillés de gestion sur les calculs commerciaux pour la Gestion Opérationnelle.

A la fin de cet article, vous saurez comment calculer une augmentation en pourcentage dans les calculs commerciaux sans aucun soucis. Si vous le souhaitez, n’hésitez pas à passer directement aux 9 exercices corrigés afin de vous entraîner.

Introduction

L’augmentation en pourcentage est une notion couramment utilisée dans divers domaines tels que les finances, les statistiques, les affaires et même dans la vie quotidienne. Que vous souhaitiez calculer l’augmentation de votre salaire, l’augmentation du prix d’un produit ou l’augmentation du nombre d’utilisateurs de votre site web, comprendre comment calculer une augmentation en pourcentage est une compétence essentielle.

L’importance de savoir calculer une augmentation en pourcentage réside dans sa capacité à fournir une image claire et précise de l’évolution d’une valeur au fil du temps. C’est un outil puissant qui peut vous aider à prendre des décisions éclairées, que ce soit pour gérer votre budget personnel, évaluer la performance d’un investissement ou analyser les tendances du marché.

Cependant, bien que le concept puisse sembler simple, le calcul d’une augmentation en pourcentage peut parfois être déroutant, surtout si vous n’êtes pas familier avec les mathématiques. C’est pourquoi nous avons créé ce guide complet pour vous aider à comprendre et à maîtriser ce calcul.

Dans ce guide, nous définirons ce qu’est une augmentation en pourcentage, expliquerons comment elle est calculée et vous guiderons à travers les étapes pour effectuer le calcul. Nous fournirons également des exemples concrets pour illustrer le processus et répondrons aux questions les plus fréquemment posées sur ce sujet. Alors, que vous soyez un étudiant, un professionnel ou simplement quelqu’un qui souhaite améliorer ses compétences en mathématiques, ce guide est pour vous.

Qu’est-ce qu’une augmentation en pourcentage

Avant de plonger dans le processus de calcul, il est important de comprendre ce qu’est une augmentation en pourcentage. En termes simples, une augmentation en pourcentage est une mesure qui indique combien une valeur a augmenté en proportion de sa valeur initiale. Elle est généralement exprimée en pourcentage, d’où son nom.

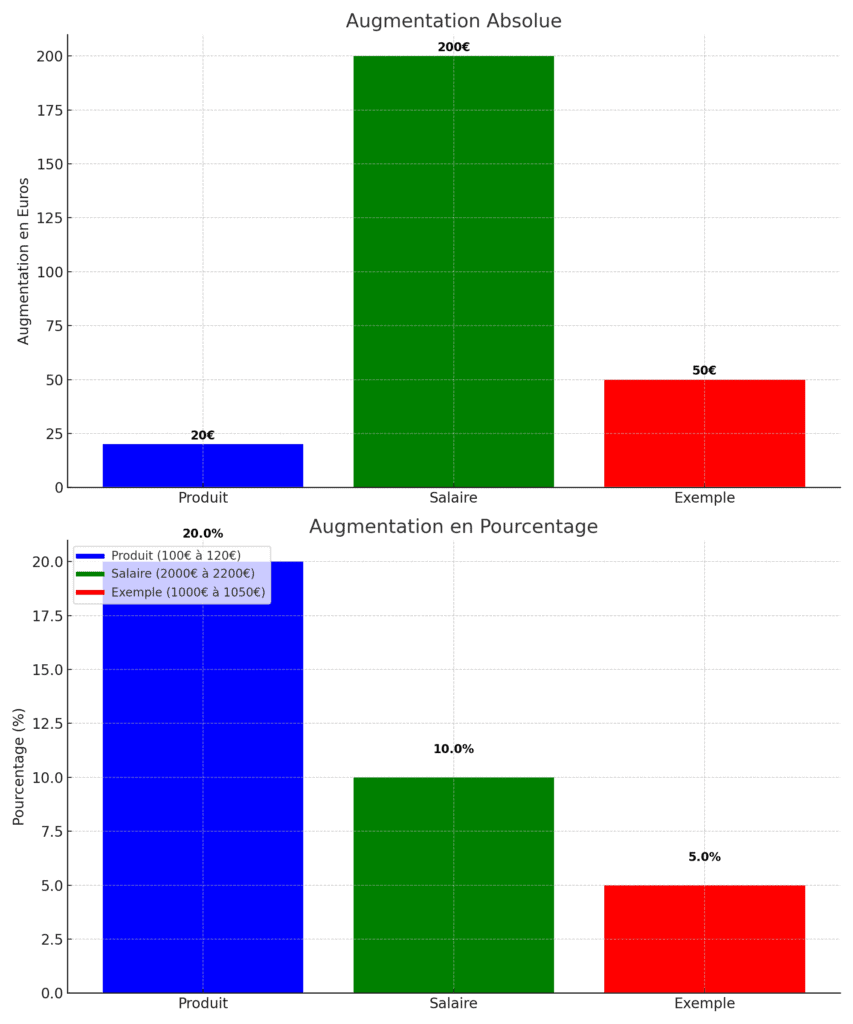
Par exemple, si le prix d’un produit passe de 100 euros à 120 euros, on peut dire qu’il a augmenté de 20%. De même, si votre salaire passe de 2 000 euros à 2 200 euros, il a augmenté de 10%. Dans ces exemples, l’augmentation en pourcentage donne une idée claire de l’ampleur de l’augmentation par rapport à la valeur initiale.

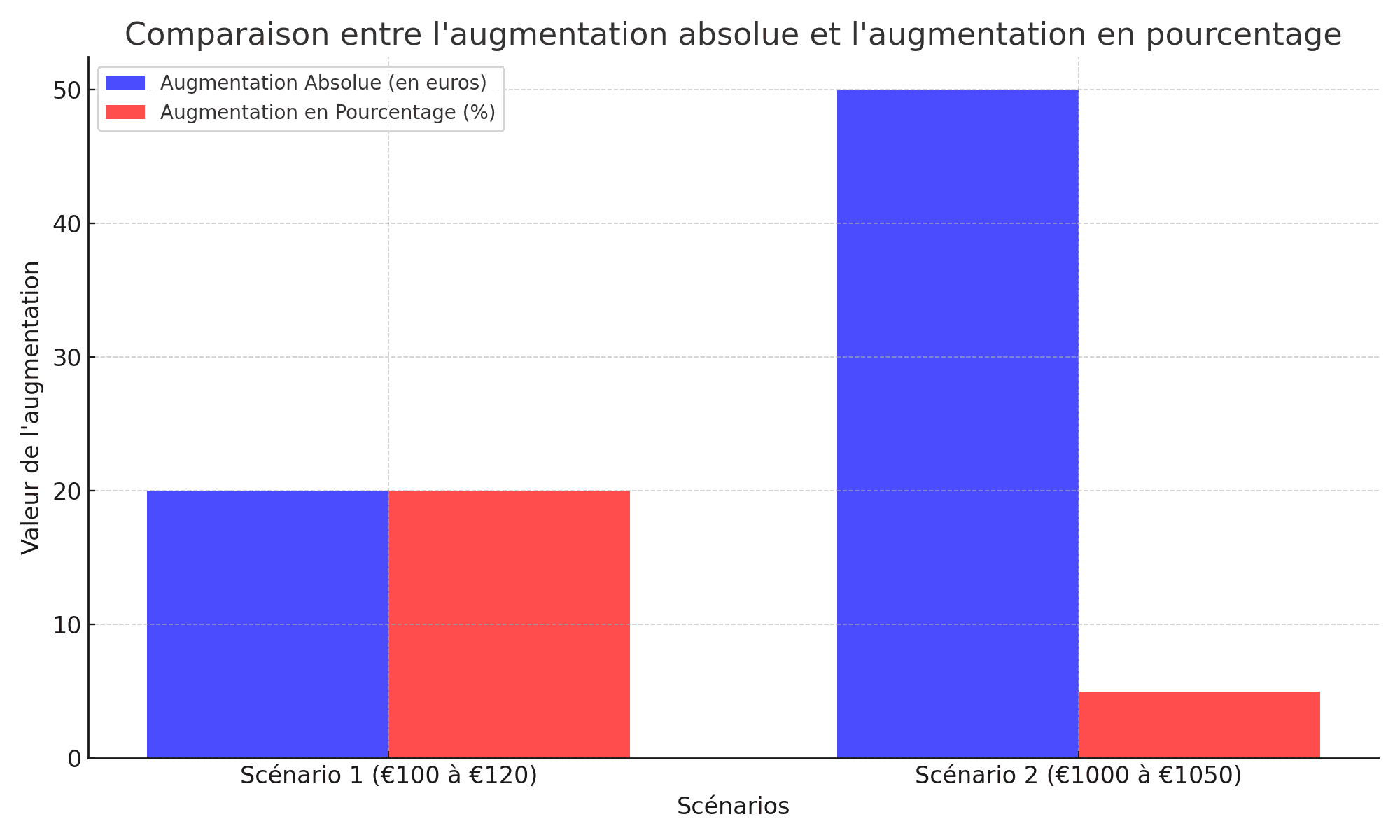
Il est important de noter que l’augmentation en pourcentage est différente de l’augmentation absolue. L’augmentation absolue est simplement la différence entre la valeur finale et la valeur initiale. Dans l’exemple du produit, l’augmentation absolue est de 20 euros (120 euros – 100 euros), tandis que l’augmentation en pourcentage est de 20%. L’augmentation en pourcentage est donc une mesure relative qui tient compte de la valeur initiale, tandis que l’augmentation absolue est une mesure absolue qui ne tient pas compte de la valeur initiale.

Comprendre cette distinction est essentiel pour interpréter correctement les augmentations en pourcentage. Par exemple, une augmentation de 50 euros peut sembler importante, mais si la valeur initiale était de 1 000 euros, l’augmentation en pourcentage n’est que de 5%, ce qui n’est pas si important. D’autre part, une augmentation de 50 euros sur une valeur initiale de 100 euros correspond à une augmentation en pourcentage de 50%, ce qui est beaucoup plus significatif.

Comment fonctionne le calcul de l’augmentation en pourcentage

Maintenant que nous avons une compréhension claire de ce qu’est une augmentation en pourcentage, il est temps de comprendre comment elle est calculée. Le calcul de l’augmentation en pourcentage repose sur une formule mathématique simple.

La formule pour calculer une augmentation en pourcentage est la suivante :

Augmentation en pourcentage = (Valeur finale – Valeur initiale) ÷ Valeur initiale x 100

Cette formule peut sembler un peu intimidante si vous n’êtes pas habitué aux mathématiques, mais elle est en fait assez simple à comprendre.

La première partie de la formule, (Valeur finale – Valeur initiale), est simplement la différence entre la valeur finale et la valeur initiale. C’est ce qu’on appelle l’augmentation absolue. Par exemple, si le prix d’un produit passe de 100 euros à 120 euros, l’augmentation absolue est de 20 euros.

La deuxième partie de la formule, ÷ Valeur initiale, consiste à diviser l’augmentation absolue par la valeur initiale. Cela donne la proportion de l’augmentation par rapport à la valeur initiale. Dans notre exemple, nous divisons l’augmentation absolue (20 euros) par la valeur initiale (100 euros), ce qui donne 0,2.

Enfin, la dernière partie de la formule, x 100, consiste à convertir cette proportion en pourcentage. Dans notre exemple, nous multiplions 0,2 par 100 pour obtenir une augmentation en pourcentage de 20%.

En utilisant cette formule, vous pouvez calculer une augmentation en pourcentage pour n’importe quelle paire de valeurs initiale et finale. C’est un outil puissant qui peut vous aider à comprendre l’évolution des valeurs au fil du temps.

Etapes pour calculer une augmentation en pourcentage

Maintenant que nous avons défini ce qu’est une augmentation en pourcentage, passons aux étapes pour calculer une augmentation en pourcentage. Le processus est assez simple et peut être accompli en trois étapes principales.

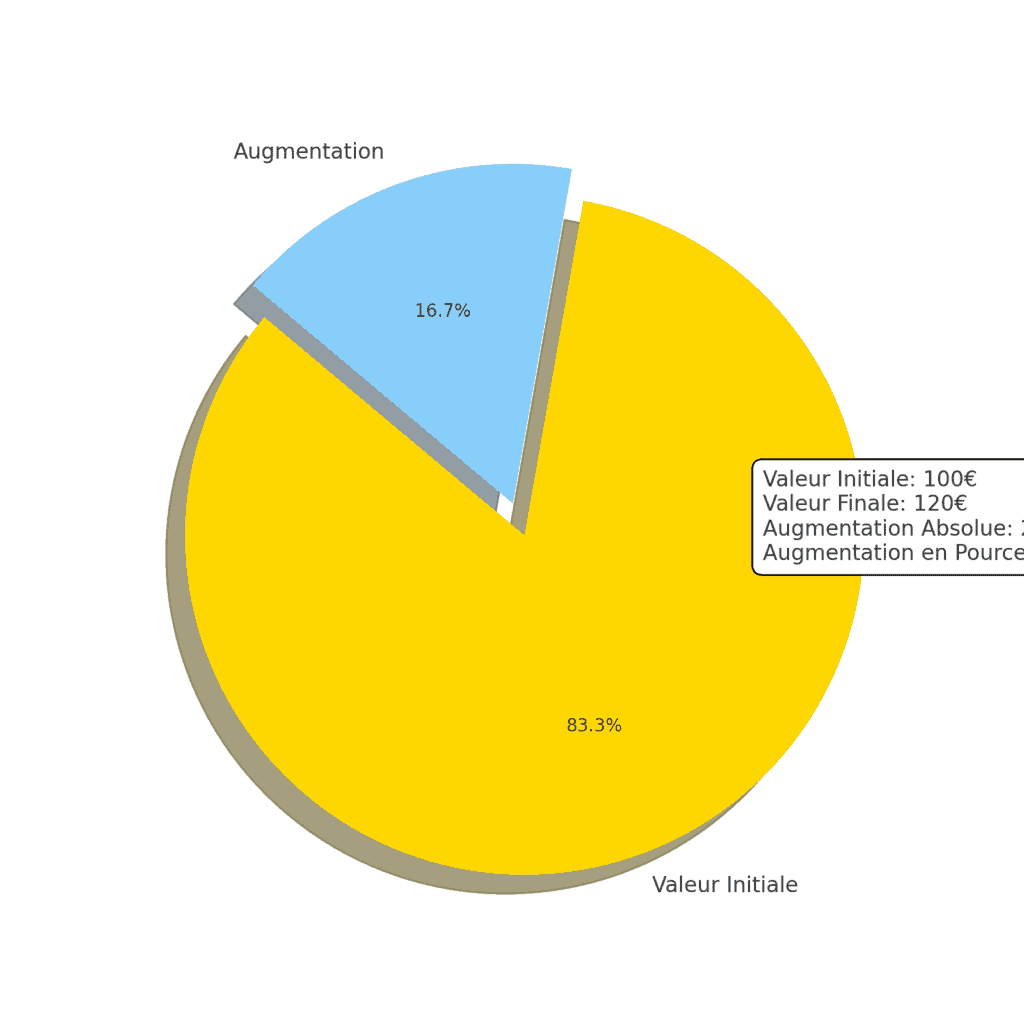
La première étape consiste à déterminer l’augmentation absolue. C’est la différence entre la valeur finale et la valeur initiale. Par exemple, si le prix d’un produit passe de 100 euros à 120 euros, l’augmentation absolue est de 20 euros (120 euros – 100 euros).

La deuxième étape consiste à diviser l’augmentation absolue par la valeur initiale. Cela donne la proportion de l’augmentation par rapport à la valeur initiale. Dans notre exemple, nous divisons l’augmentation absolue (20 euros) par la valeur initiale (100 euros), ce qui donne 0,2.

La troisième et dernière étape consiste à convertir cette proportion en pourcentage. Pour ce faire, nous multiplions la proportion par 100. Dans notre exemple, nous multiplions 0,2 par 100 pour obtenir une augmentation en pourcentage de 20%.

Il est important de noter que ces étapes s’appliquent à toutes les augmentations en pourcentage, qu’il s’agisse d’une augmentation de prix, d’une augmentation de salaire ou d’une augmentation du nombre d’utilisateurs d’un site web. La clé est de toujours commencer par la valeur initiale et de travailler à partir de là.

En suivant ces étapes, vous pouvez calculer avec précision une augmentation en pourcentage. Cependant, il est également important de comprendre comment interpréter le résultat, ce que nous aborderons dans la section suivante.

Exemples de calcul d’augmentation en pourcentage

Pour illustrer le processus de calcul de l’augmentation en pourcentage, examinons quelques exemples concrets.

Exemple 1: Supposons que vous ayez reçu une augmentation de salaire. Votre salaire initial était de 2000 euros par mois et votre nouveau salaire est de 2 200 euros par mois. Quelle est l’augmentation en pourcentage de votre salaire ?

1. Calculez l’augmentation absolue : 2 200 euros – 2 000 euros = 200 euros
2. Divisez l’augmentation absolue par la valeur initiale : 200 euros ÷ 2 000 euros = 0,1
3. Convertissez cette proportion en pourcentage : 0,1 x 100 = 10%

Donc, votre salaire a augmenté de 10%.

Exemple 2: Vous êtes propriétaire d’une entreprise et vous constatez que le nombre de clients a augmenté de 500 à 650 au cours du dernier mois. Quelle est l’augmentation en pourcentage du nombre de clients ?

1. Calculez l’augmentation absolue : 650 clients – 500 clients = 150 clients
2. Divisez l’augmentation absolue par la valeur initiale : 150 clients ÷ 500 clients = 0,3
3. Convertissez cette proportion en pourcentage : 0,3 x 100 = 30%

Donc, le nombre de clients a augmenté de 30%.

Ces exemples montrent comment le calcul de l’augmentation en pourcentage peut être appliqué à diverses situations. Que vous calculiez une augmentation de salaire, une augmentation du nombre de clients ou toute autre augmentation, le processus est le même. Il suffit de suivre les étapes et d’utiliser la formule correctement.

Comment interpréter le résultat du calcul

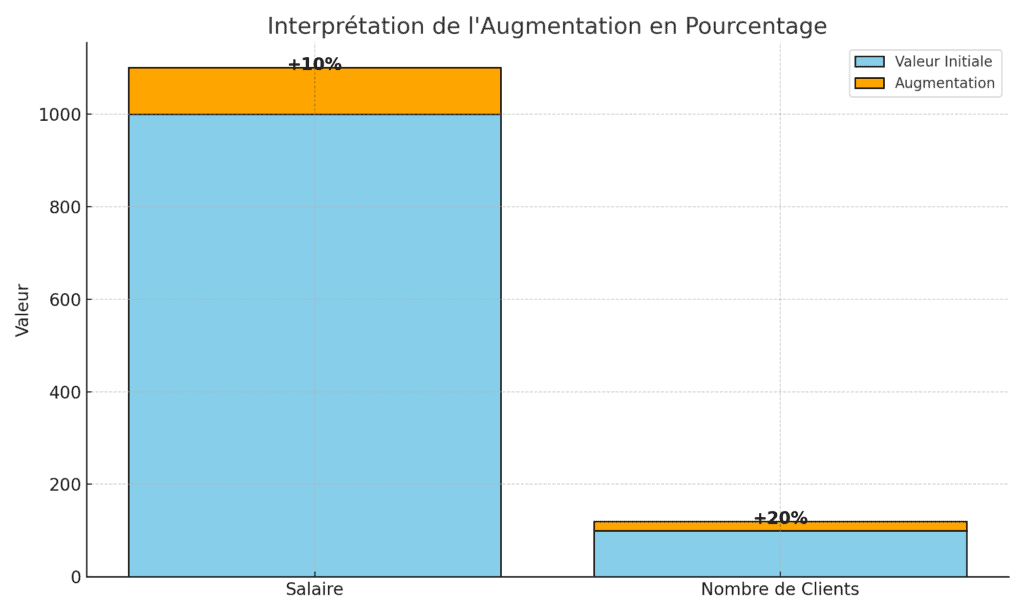
Une fois que vous avez calculé une augmentation en pourcentage, il est tout aussi important de savoir comment interpréter le résultat. L’augmentation en pourcentage donne une indication de l’ampleur de l’augmentation par rapport à la valeur initiale.

Par exemple, si vous calculez une augmentation de salaire et que vous obtenez un résultat de 10%, cela signifie que votre salaire a augmenté de 10% par rapport à votre salaire initial. En d’autres termes, pour chaque 100 euros de votre salaire initial, vous avez reçu une augmentation de 10 euros.

De même, si vous êtes propriétaire d’une entreprise et que vous calculez une augmentation de 20% du nombre de clients, cela signifie que pour chaque 100 clients que vous aviez initialement, vous avez gagné 20 clients supplémentaires.

Il est important de noter que l’augmentation en pourcentage est une mesure relative, pas absolue. Une augmentation de 50% signifie que la valeur finale est 50% plus grande que la valeur initiale, pas qu’elle est 50% de la valeur initiale. Par exemple, si le prix d’un produit passe de 100 euros à 150 euros, l’augmentation en pourcentage est de 50%, pas de 150%.

Enfin, il est également important de comprendre que l’augmentation en pourcentage ne donne pas d’information sur la durée pendant laquelle l’augmentation s’est produite. Une augmentation de 20% pourrait se produire sur une période d’un mois, d’un an ou de dix ans. Pour obtenir des informations sur la vitesse ou le taux d’augmentation, vous devrez effectuer des calculs supplémentaires, tels que le calcul du taux de croissance annuel composé.

Erreurs courantes lors du calcul de l’augmentation en pourcentage

Lors du calcul de l’augmentation en pourcentage, il est important de faire attention à certaines erreurs courantes. En étant conscient de ces erreurs et en sachant comment les éviter, vous pouvez vous assurer d’obtenir des résultats précis.

La première erreur courante est de confondre l’augmentation absolue avec l’augmentation en pourcentage. Comme nous l’avons mentionné précédemment, l’augmentation absolue est simplement la différence entre la valeur finale et la valeur initiale, tandis que l’augmentation en pourcentage est cette différence exprimée en pourcentage de la valeur initiale. Assurez-vous de ne pas confondre ces deux concepts.

Une autre erreur courante est d’utiliser la valeur finale au lieu de la valeur initiale dans la formule de calcul. Rappelez-vous que l’augmentation en pourcentage est calculée par rapport à la valeur initiale, pas à la valeur finale. Par exemple, si le prix d’un produit passe de 100 euros à 120 euros, vous devez diviser l’augmentation absolue (20 euros) par la valeur initiale (100 euros), pas par la valeur finale (120 euros).

Enfin, une autre erreur courante est de ne pas convertir la proportion en pourcentage à la fin du calcul. Après avoir divisé l’augmentation absolue par la valeur initiale, vous obtenez une proportion, pas un pourcentage. Pour convertir cette proportion en pourcentage, vous devez la multiplier par 100.

En évitant ces erreurs courantes, vous pouvez vous assurer que vos calculs d’augmentation en pourcentage sont précis et significatifs. N’oubliez pas que la pratique est la clé pour maîtriser ce calcul, alors n’hésitez pas à vous exercer avec différents exemples jusqu’à ce que vous vous sentiez à l’aise.

Utilisation de l’augmentation en pourcentage dans la vie quotidienne

Le calcul de l’augmentation en pourcentage est une compétence utile dans de nombreux aspects de la vie quotidienne. Voici quelques exemples de situations où vous pourriez avoir besoin de calculer une augmentation en pourcentage.

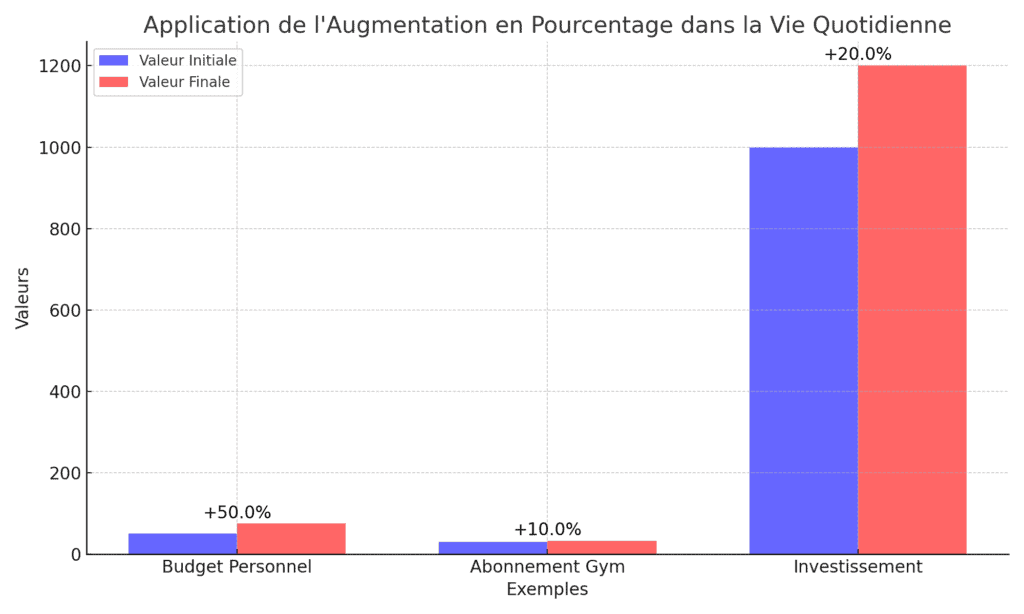
Premièrement, le calcul de l’augmentation en pourcentage peut vous aider à gérer votre budget personnel. Par exemple, si vous suivez vos dépenses et que vous remarquez que vos dépenses d’épicerie ont augmenté de 50 euros à 75 euros, vous pouvez calculer l’augmentation en pourcentage pour comprendre l’ampleur de cette augmentation. Dans ce cas, l’augmentation en pourcentage est de 50%, ce qui pourrait vous inciter à revoir vos habitudes d’achat pour réduire vos dépenses.

Deuxièmement, le calcul de l’augmentation en pourcentage peut vous aider à évaluer les augmentations de prix. Par exemple, si le prix de votre abonnement à la salle de sport passe de 30 euros par mois à 33 euros par mois, l’augmentation en pourcentage est de 10%. Cette information peut vous aider à décider si l’augmentation de prix est raisonnable et si vous souhaitez continuer votre abonnement.

Troisièmement, le calcul de l’augmentation en pourcentage peut vous aider à comprendre l’évolution de votre situation financière. Par exemple, si vous investissez de l’argent et que la valeur de votre investissement passe de 1000 euros à 1200 euros, l’augmentation en pourcentage est de 20%. Cette information peut vous aider à évaluer la performance de votre investissement et à prendre des décisions financières éclairées.

Ces exemples montrent comment le calcul de l’augmentation en pourcentage peut être appliqué à divers aspects de la vie quotidienne. En maîtrisant ce calcul, vous pouvez améliorer votre gestion financière et prendre des décisions plus éclairées.

Utilisation de l’augmentation en pourcentage dans le milieu professionnel

Dans le milieu professionnel, le calcul de l’augmentation en pourcentage est également un outil précieux. Il peut être utilisé dans divers contextes, allant de l’évaluation de la performance à l’analyse des tendances du marché. Voici quelques exemples.

Premièrement, si vous êtes un gestionnaire, vous pouvez utiliser le calcul de l’augmentation en pourcentage pour évaluer la performance de votre équipe. Par exemple, si le nombre de projets terminés par votre équipe passe de 10 à 15 en un mois, l’augmentation en pourcentage est de 50%. Cette information peut vous aider à comprendre l’efficacité de votre équipe et à identifier les domaines qui nécessitent une amélioration.

Deuxièmement, si vous travaillez dans le domaine des ventes ou du marketing, vous pouvez utiliser le calcul de l’augmentation en pourcentage pour analyser les tendances du marché. Par exemple, si les ventes d’un produit passent de 1 000 unités à 1 200 unités en un mois, l’augmentation en pourcentage est de 20%. Cette information peut vous aider à comprendre la demande du marché pour ce produit et à planifier vos stratégies de vente et de marketing en conséquence.

Troisièmement, si vous travaillez dans le domaine de la finance, vous pouvez utiliser le calcul de l’augmentation en pourcentage pour évaluer la performance des investissements. Par exemple, si la valeur d’un investissement passe de 10 000 euros à 11 000 euros en un an, l’augmentation en pourcentage est de 10%. Cette information peut vous aider à évaluer la rentabilité de l’investissement et à prendre des décisions financières éclairées.

Ces exemples montrent comment le calcul de l’augmentation en pourcentage peut être utilisé dans divers contextes professionnels. En maîtrisant ce calcul, vous pouvez améliorer votre capacité à évaluer la performance, à analyser les tendances du marché et à prendre des décisions éclairées.

Outils en ligne pour calculer une augmentation en pourcentage

Si vous préférez éviter les calculs manuels, il existe plusieurs outils en ligne gratuits qui peuvent vous aider à calculer une augmentation en pourcentage. Ces outils sont faciles à utiliser et peuvent vous fournir des résultats précis en quelques secondes. Voici quelques exemples.

1. Calculatrices en ligne : Il existe de nombreuses calculatrices en ligne gratuites qui peuvent calculer une augmentation en pourcentage. Vous n’avez qu’à entrer la valeur initiale et la valeur finale, et la calculatrice fera le reste. Certains de ces outils offrent également des explications détaillées du calcul, ce qui peut être utile si vous essayez de comprendre le processus.
   
   
2. Feuilles de calcul : Si vous avez besoin de calculer des augmentations en pourcentage pour un grand nombre de valeurs, une feuille de calcul peut être un outil précieux. Vous pouvez utiliser des logiciels comme Microsoft Excel ou Google Sheets pour créer une formule qui calcule l’augmentation en pourcentage. Une fois que vous avez créé la formule, vous pouvez l’appliquer à toutes les valeurs de votre feuille de calcul.
   
   
3. Applications mobiles : Si vous avez besoin de calculer une augmentation en pourcentage en déplacement, il existe plusieurs applications mobiles qui peuvent vous aider. Ces applications fonctionnent de la même manière que les calculatrices en ligne, mais elles sont conçues pour être utilisées sur un smartphone ou une tablette.

Ces outils peuvent vous faire gagner du temps et vous aider à éviter les erreurs de calcul. Cependant, il est toujours utile de comprendre comment le calcul est effectué, afin de pouvoir interpréter correctement les résultats.

FAQ: Questions fréquemment posées sur le calcul de l’augmentation en pourcentage

Il est tout à fait normal d’avoir des questions sur le calcul de l’augmentation en pourcentage. Voici quelques-unes des questions les plus fréquemment posées sur ce sujet, ainsi que leurs réponses.

1. Question : Que signifie une augmentation en pourcentage de 100% ?
   • Réponse : Une augmentation en pourcentage de 100% signifie que la valeur finale est deux fois la valeur initiale. Par exemple, si le prix d’un produit passe de 50 euros à 100 euros, l’augmentation en pourcentage est de 100%.
     
     
2. Question : Comment calculer une augmentation en pourcentage si la valeur initiale est zéro ?
   • Réponse : Si la valeur initiale est zéro, l’augmentation en pourcentage est généralement considérée comme infinie, car toute augmentation par rapport à zéro est une augmentation infinie en pourcentage. Dans la pratique, cependant, il est souvent plus utile de simplement indiquer l’augmentation absolue.
     
     
3. Question : Est-ce que l’augmentation en pourcentage est la même chose que le taux de croissance ?
   • Réponse : L’augmentation en pourcentage et le taux de croissance sont des concepts similaires, mais ils ne sont pas exactement les mêmes. L’augmentation en pourcentage mesure l’ampleur de l’augmentation par rapport à la valeur initiale, tandis que le taux de croissance mesure la vitesse de l’augmentation sur une période de temps spécifique.
     
     
4. Question : Comment calculer l’augmentation en pourcentage si la valeur finale est inférieure à la valeur initiale ?
   • Réponse : Si la valeur finale est inférieure à la valeur initiale, l’augmentation en pourcentage sera négative. Cela indique une diminution plutôt qu’une augmentation. Par exemple, si le prix d’un produit passe de 100 euros à 80 euros, l’augmentation en pourcentage est de -20%.

Ces réponses devraient vous aider à mieux comprendre le calcul de l’augmentation en pourcentage. N’oubliez pas que la pratique est la clé pour maîtriser ce calcul, alors n’hésitez pas à vous exercer avec différents exemples jusqu’à ce que vous vous sentiez à l’aise.

Conclusion

En conclusion, savoir comment calculer une augmentation en pourcentage est une compétence précieuse qui peut être utilisée dans de nombreux aspects de la vie quotidienne et professionnelle. Que ce soit pour évaluer une augmentation de salaire, analyser les tendances du marché ou gérer votre budget personnel, l’augmentation en pourcentage est un outil puissant pour comprendre l’évolution des valeurs au fil du temps.

Le processus de calcul est assez simple et repose sur une formule mathématique de base. Cependant, il est important de faire attention aux erreurs courantes, comme la confusion entre l’augmentation absolue et l’augmentation en pourcentage, l’utilisation de la valeur finale au lieu de la valeur initiale dans la formule, et l’oubli de convertir la proportion en pourcentage à la fin du calcul.

Il est également important de savoir comment interpréter le résultat du calcul. Une augmentation en pourcentage de 20% signifie que la valeur finale est 20% plus grande que la valeur initiale, pas qu’elle est 20% de la valeur initiale. De plus, l’augmentation en pourcentage ne donne pas d’information sur la durée pendant laquelle l’augmentation s’est produite.

Enfin, si vous préférez éviter les calculs manuels, il existe plusieurs outils en ligne gratuits qui peuvent vous aider à calculer une augmentation en pourcentage. Ces outils sont faciles à utiliser et peuvent vous fournir des résultats précis en quelques secondes.

Nous espérons que ce guide vous a aidé à comprendre comment calculer une augmentation en pourcentage. N’oubliez pas que la pratique est la clé pour maîtriser ce calcul, alors n’hésitez pas à vous exercer avec différents exemples jusqu’à ce que vous vous sentiez à l’aise. Bonne chance !

9 Exercices corrigés pour calculer une augmentation en pourcentage

Application Burger House

Énoncé :

Dans la ville de Pau, le franchiseur d’une chaîne de restaurants de burger réputée « Burger House » envisage d’augmenter les prix de ses menus. Face à une forte demande et une augmentation des coûts de production, il décide de faire une révision de ses tarifs de vente. Avant toute décision, il souhaite évaluer l’impact que chaque augmentation de prix aurait sur ses différentes marges (marge unitaire, marge sur coûts variables, marge sur coûts fixes).

Pour cela, il dispose des informations suivantes :
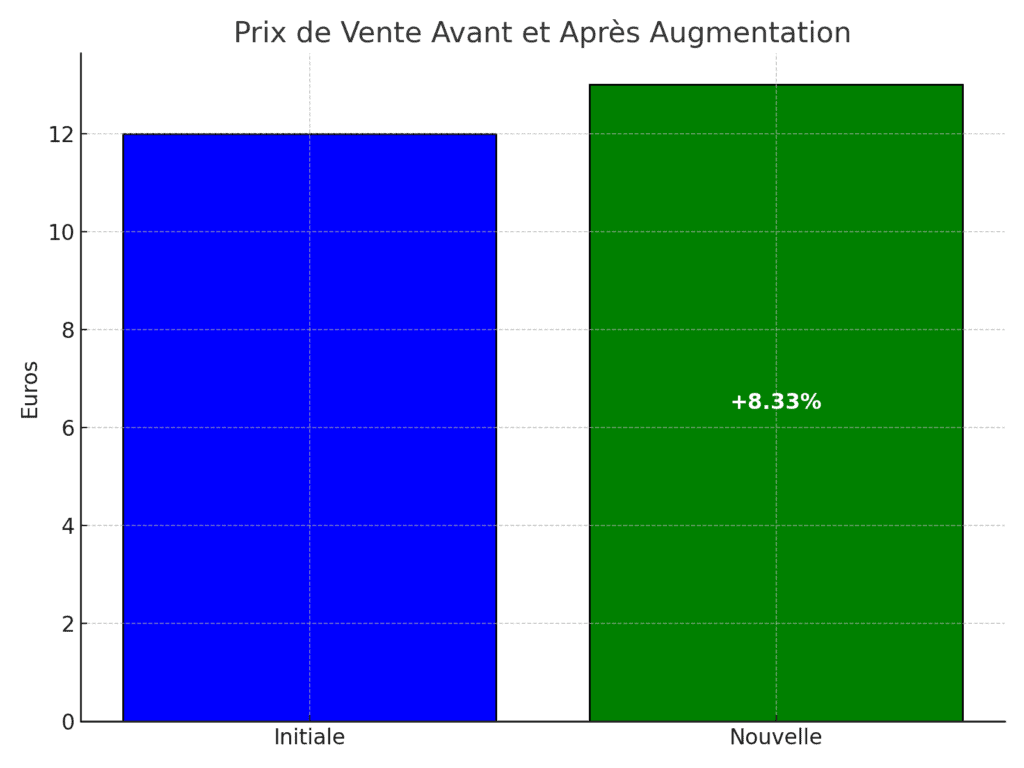
– Prix de vente initial du menu standard (PV initial) = 12,00 €
– Prix d’achat unitaire du menu standard (PA) = 5,00 €
– Quantité vendue actuellement = 10 000 units
– Coûts fixes annuels = 50 000 €
– Coûts variables unitaires = 2,50 €

Travail à faire :

1) Calculez la marge unitaire et marge globale avant l’augmentation de prix.
2) Si le franchiseur décide d’augmenter le prix du menu standard de 1 €, calculez la nouvelle marge unitaire et la nouvelle marge globale.
3) Quel est le pourcentage d’augmentation du prix de vente ?
4) Calculez le pourcentage d’augmentation de la marge unitaire.
5) Calculez le pourcentage d’augmentation de la marge globale.

Proposition de correction :

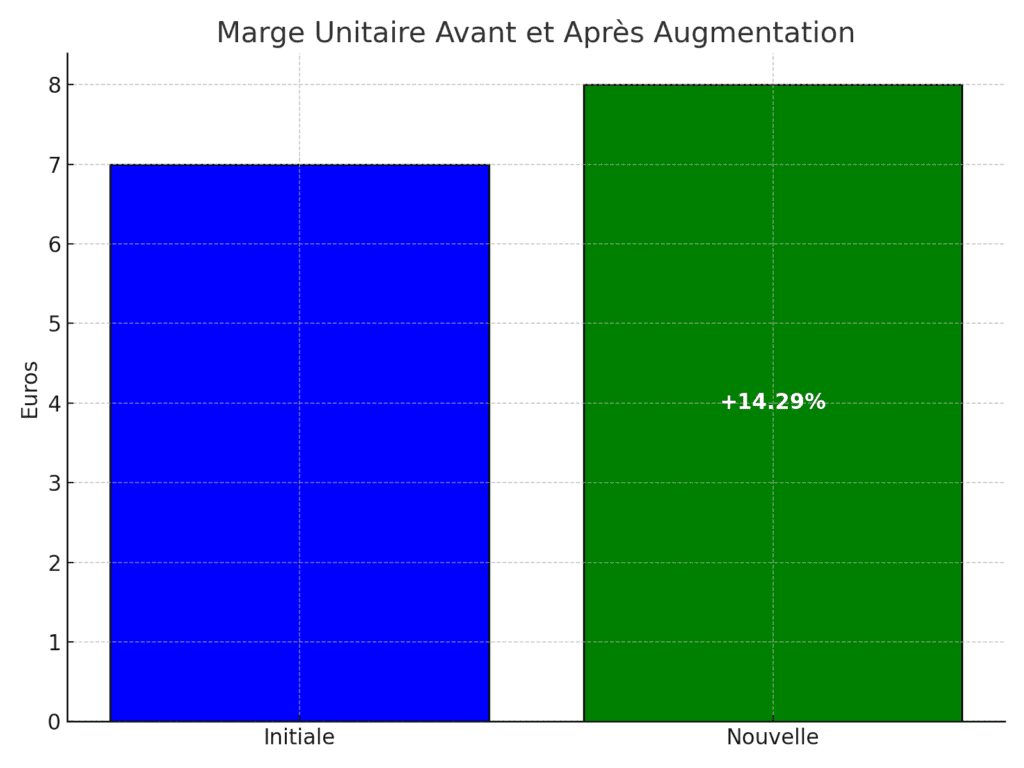
1) La marge unitaire se calcule comme la différence entre le prix de vente et le prix d’achat. Ici, Marge unitaire = PV initial – PA = 12,00 € – 5,00 € = 7,00 €

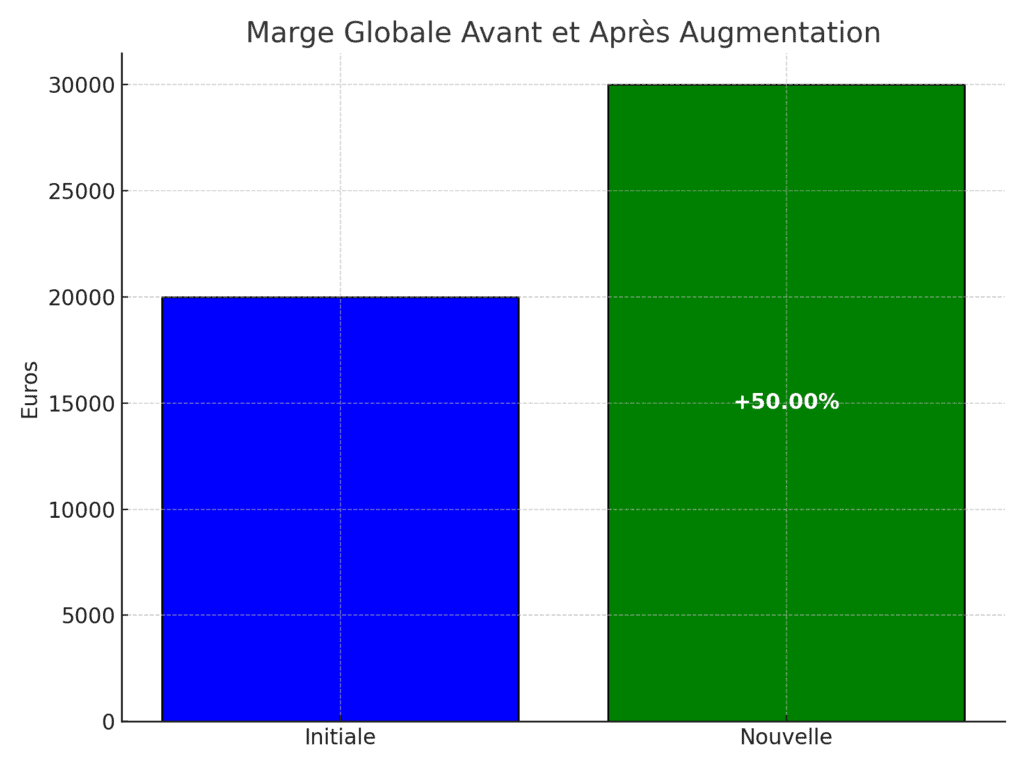
La marge globale se calcule comme le produit de la marge unitaire et la quantité vendue. Ici, Marge globale = Marge unitaire x Quantité Vendu = 7,00 € x 10 000 = 70 000 €

2) Avec l’augmentation de 1 €, le nouveau prix de vente sera de 13,00 €. La nouvelle marge unitaire sera donc de 13,00 € – 5,00 € = 8,00 €.

La nouvelle marge globale sera de 8,00 € x 10 000 = 80 000 €

3) Le pourcentage d’augmentation du prix de vente est donné par la formule : ((Nouveau PV – Ancien PV) ? Ancien PV) x 100.
Donc, ((13,00 € – 12,00 €) / 12,00 €) x 100 = 8,33%

4) Le pourcentage d’augmentation de la marge unitaire est donné par la formule : ((Nouvelle marge unitaire – Ancienne marge unitaire) ? Ancienne marge unitaire) x 100.
Donc, ((8,00 € – 7,00 €) / 7,00 €) x 100 = 14,29%

5) Le pourcentage d’augmentation de la marge globale est donné par la formule : ((Nouvelle marge globale – Ancienne marge globale) ? Ancienne marge globale) x 100.
Donc, ((80 000 € – 70 000 €) / 70 000 €) x 100 = 14,29%

Récapitulatif des Formules Utilisées :

– Marge unitaire = Prix de vente – Prix d’achat
– Marge globale = Marge unitaire x Quantité Vendu
– Pourcentage d’augmentation = ((Nouvelle valeur – Ancienne valeur) ? Ancienne valeur) x 100.

Application Fruits Éclatants

Énoncé :

L’entreprise « Fruits Éclatants », spécialisée dans la vente de fruits frais, envisage d’augmenter le prix de ses pommes. Leur prix actuel est de 2,00 € par kilogramme.

Au cours des derniers jours, l’entreprise a reçu des informations sur l’augmentation des coûts de production et de transport des pommes par ses fournisseurs. Par conséquent, ils ont décidé d’ajuster le prix des pommes.

Travail à faire :

1. Si « Fruits Éclatants » décide d’augmenter le prix des pommes de 10%, quel sera le nouveau prix ?
2. Quel est le montant de l’augmentation en euros ?
3. Si l’entreprise décide de réduire le prix augmenté de 5%, quel sera alors le nouveau prix?
4. Combien le prix a-t-il diminué en euros depuis l’augmentation précédente de 10% ?
5. Quel est le pourcentage de réduction par rapport au prix augmenté de 10% ?

Proposition de correction :

1. Pour calculer le nouveau prix après une augmentation de 10%, nous utilisons la formule : nouveau prix = prix actuel + (prix actuel x taux d’augmentation)
Soit : nouveau prix = 2,00 € + (2,00 € x 10%) = 2,00 € + 0,20 € = 2,20 €

2. Le montant de l’augmentation en euros est donc de : 2,20 € – 2,00 € = 0,20 €

3. Pour réduire le prix augmenté de 5%, nous utilisons la formule : nouveau prix = prix augmenté – (prix augmenté x taux de réduction)
Soit : nouveau prix = 2,20 € – (2,20 € x 5%) = 2,20 € – 0,11 € = 2,09 €

4. Le prix a diminué de : 2,20 € – 2,09 € = 0,11 € depuis l’augmentation précédente de 10%.

5. Le pourcentage de réduction par rapport au prix augmenté de 10% est de : (0,11 € ÷ 2,20 €) x 100 = 5%

Récapitulatif des Formules Utilisées :

– Augmentation: nouveau prix = prix actuel + (prix actuel x taux d’augmentation)
– Récupérer l’augmentation en euros: Augmentation en euros = prix après augmentation – prix avant augmentation
– Réduction: nouveau prix = prix actuel – (prix actuel x taux de réduction)
– Récupérer la réduction en euros: Réduction en euros = prix avant réduction – prix après réduction
– Conversion de la réduction en pourcentage: (réduction en euros ÷ prix avant réduction) x 100

Application Paris Chaussures

Énoncé :

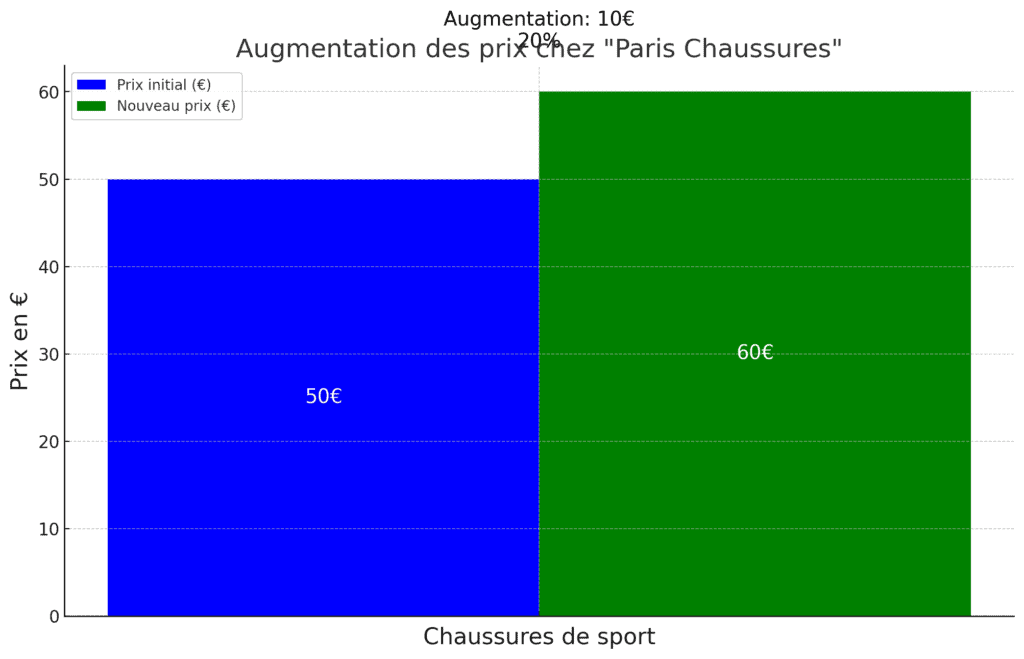
Monsieur Durand est le gérant d’une petite entreprise de ventes de chaussures, appelée « Paris Chaussures ». Il vient d’appliquer une augmentation de prix sur plusieurs articles dans sa boutique pour répondre à l’augmentation des coûts de production et du marché. Monsieur Durand a besoin d’aide pour calculer le pourcentage de cette augmentation.

Un exemple d’articles concernés seraient des chaussures de sport qui coûtaient initialement 50 € et qui sont maintenant vendus à 60 €.

Travail à faire :

1. Quel est le montant de l’augmentation en € ?
2. Comment calculer le pourcentage de l’augmentation à partir du prix initial ?
3. Quel est le pourcentage de l’augmentation ?
4. Comment calculer le nouveau prix après augmentation à partir du prix initial et du pourcentage d’augmentation ?
5. En reprenant l’exemple des chaussures de sport, quel serait le nouveau prix si Monsieur Durand décidait d’appliquer une augmentation de 20%?

Proposition de correction :

1. Le montant de l’augmentation est calculé en soustrayant le prix initial du nouveau prix. Donc, ici, l’augmentation est de 60 € – 50 € = 10 €.

2. Le pourcentage de l’augmentation est calculé en divisant le montant de l’augmentation par le prix initial et en multipliant le résultat par 100. La formule est donc : (augmentation ? Prix initial) x 100 = % d’augmentation.

3. En utilisant cette formule, le pourcentage de l’augmentation sur les chaussures de sport est donc de : (10 € ? 50 €) x 100 = 20%.

4. Le nouveau prix après augmentation est calculé en ajoutant le pourcentage de l’augmentation au prix initial. La formule est donc : Prix initial + (Prix initial x % d’augmentation ? 100) = Nouveau prix.

5. Si Monsieur Durand décidait d’appliquer une augmentation de 20%, le nouveau prix des chaussures de sport serait donc de : 50 € + (50 € x 20 ? 100) = 60 €.

Récapitulatif des Formules Utilisées :

– Montant de l’augmentation : Nouveau prix – Prix initial.
– Pourcentage de l’augmentation : (Augmentation ? Prix initial) x 100.
– Nouveau prix après augmentation : Prix initial + (Prix initial x % d’augmentation ? 100).

Application TechnoStore

Énoncé :

L’entreprise « TechnoStore », spécialisée dans la vente de produits électroniques, a connu une augmentation significative de ses ventes au cours de l’année précédente. Elle souhaite calculer le pourcentage de cette augmentation pour chacun de ses produits phares : un ordinateur portable, un smartphone et une tablette.

– Au départ, TechnoStore a vendu 200 ordinateurs à 750 € l’unité. Vers la fin de l’année, ils ont réussi à vendre 250 de ces mêmes ordinateurs.
– Pour les smartphones, ils en ont vendu 300 à 600 € chacun au départ. Vers la fin de l’année, ils ont vendu 360 smartphones.
– En début d’année, 180 tablettes ont été vendues à 400 € chacune. Vers la fin de l’année, ils ont réussi à vendre 220 tablettes.

Travail à faire :

1. Quel est le pourcentage d’augmentation des ventes d’ordinateurs ?
2. Quel est le pourcentage d’augmentation des ventes de smartphones ?
3. Quel est le pourcentage d’augmentation des ventes de tablettes ?
4. En moyenne, de combien le pourcentage des ventes a-t-il augmenté ?
5. Laquelle des trois catégories de produits présente la plus grande augmentation en pourcentage ?

Proposition de correction :

1. Pour calculer le pourcentage d’augmentation des ventes d’ordinateurs, nous appliquons la formule : ((Nouvelle quantité – Ancienne quantité) / Ancienne Quantité) x 100. Ici, cela donne ((250 – 200) ÷ 200) x 100 = 25% d’augmentation

2. Pour calculer le pourcentage d’augmentation des ventes de smartphones, nous appliquons la formule : ((Nouvelle quantité – Ancienne quantité) / Ancienne Quantité) x 100. Ici, cela donne ((360 – 300) ÷ 300) x 100 = 20% d’augmentation

3. Pour calculer le pourcentage d’augmentation des ventes de tablettes, nous appliquons la formule : ((Nouvelle quantité – Ancienne quantité) / Ancienne Quantité) x 100. Ici, cela donne ((220 – 180) ÷ 180) x 100 = 22,22% d’augmentation

4. Pour calculer l’augmentation moyenne, nous faisons la moyenne des trois pourcentages, c’est-à-dire (25 + 20 + 22,22) / 3 = 22,41% d’augmentation moyenne

5. Les ordinateurs présentent la plus grande augmentation en pourcentage de 25%.

Récapitulatif des Formules Utilisées :

Pourcentage d’augmentation = ((Nouvelle quantité – Ancienne quantité) ÷ Ancienne Quantité) x 100

Moyenne de pourcentage d’augmentation = (Pourcentage d’augmentation 1 + Pourcentage d’augmentation 2 + Pourcentage d’augmentation 3) ÷ Nombre de catégories

Application Le Soleil Doré

Énoncé :

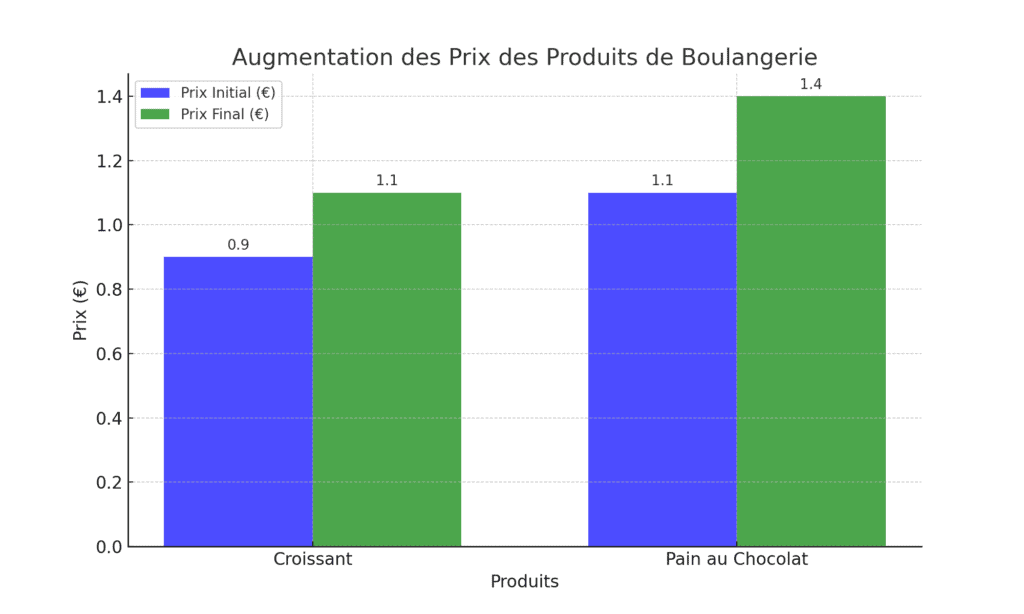
L’entreprise « Le Soleil Doré », spécialisée dans la vente de produits de boulangerie, souhaite évaluer l’impact d’une augmentation sur ses prix. Ils ont augmenté le prix de leur croissant de 0,90 € à 1,10 € et celui de leur pain au chocolat de 1,10 € à 1,40 €. Les coûts de production n’ont, quant à eux, pas augmenté.

Travail à faire :

1. Quel est le pourcentage d’augmentation du prix du croissant ?
2. Quel est le pourcentage d’augmentation du prix du pain au chocolat ?
3. Quel est l’effet de ces augmentations sur la marge unitaire de chaque produit ?
4. Quel est le nouvel indice de prix pour le croissant et le pain au chocolat, si l’indice initial était de 100 pour les deux ?
5. Si l’entreprise vendait 1000 croissants et 800 pains au chocolat par jour, quel serait l’impact de ces augmentations sur son chiffre d’affaires journalier ?

Proposition de correction :

1. Pourcentage d’augmentation du prix du croissant = ((Prix final – Prix initial) / Prix initial) x 100
= ((1,10 € – 0,90 €) / 0,90 €) x 100 = 22,22%
2. Pourcentage d’augmentation du prix du pain au chocolat = ((Prix final – Prix initial) / Prix initial) x 100
= ((1,40 € – 1,10 €) / 1,10 €) x 100 = 27,27%
3. L’augmentation du prix de vente sans une hausse du coût de production entraîne une augmentation de la marge unitaire. La marge unitaire est désormais la différence entre le nouveau prix de vente et le coût de production initial.
4. Indice de prix = (Prix final / Prix initial) x 100
Pour le croissant : (1,10 € / 0,90 €) x 100 = 122,22
Pour le pain au chocolat : (1,40 € / 1,10 €) x 100 = 127,27
5. Impact sur le chiffre d’affaires :
Pour le croissant : (1,10 € – 0,90 €) x 1000 = 200 € supplémentaires par jour.
Pour le pain au chocolat : (1,40 € – 1,10 €) x 800 = 240 € supplémentaires par jour.

Récapitulatif des Formules Utilisées :

– Pourcentage d’augmentation = ((Prix final – Prix initial) / Prix initial) x 100
– Indice de prix = (Prix final / Prix initial) x 100
– Impact sur le chiffre d’affaires : (Prix final – Prix initial) x quantité vendue

Application ABC Fashion

Énoncé :

L’entreprise ABC Fashion est spécialisée dans la vente de vêtements de mode. Au début de l’année, le gérant a décidé d’augmenter le prix de certains articles. Vous êtes l’assistant du gérant et on vous demande de déterminer l’augmentation en pourcentage des différents produits. Voici quelques informations :

1) Le prix d’un pull est passé de 30 € à 35 €.
2) Le prix d’un pantalon est passé de 45 € à 50 €.
3) Le prix d’une robe est passé de 55 € à 65 €.
4) Le prix d’un manteau est passé de 120 € à 130 €.
5) Le prix d’une chemise est passé de 15 € à 18 €.

Travail à faire :

1) Quel est le pourcentage d’augmentation du prix du pull ?
2) Quel est le pourcentage d’augmentation du prix du pantalon ?
3) Quel est le pourcentage d’augmentation du prix de la robe ?
4) Quel est le pourcentage d’augmentation du prix du manteau ?
5) Quel est le pourcentage d’augmentation du prix de la chemise ?

Proposition de correction :

1) L’augmentation du pull est de 5 €. Pour déterminer le pourcentage d’augmentation, nous utilisons la formule : [(Pf – Pi) / Pi] x 100, où Pf est le prix final et Pi le prix initial. Donc, (5 ÷ 30) x 100 = 16,67%. Le prix du pull a donc augmenté de 16,67%.

2) L’augmentation du pantalon est de 5 €. En utilisant la même formule, (5 ÷ 45) x 100 = 11,11%. Le prix du pantalon a donc augmenté de 11,11%.

3) L’augmentation de la robe est de 10 €. Donc, (10 ÷ 55) x 100 = 18,18%. Le prix de la robe a donc augmenté de 18,18%.

4) L’augmentation du manteau est de 10 €. Donc, (10 ÷ 120) x 100 = 8,33%. Le prix du manteau a donc augmenté de 8,33%.

5) L’augmentation de la chemise est de 3 €. Donc, (3 ÷ 15) x 100 = 20%. Le prix de la chemise a donc augmenté de 20%.

Récapitulatif des Formules Utilisées :

– Formule de l’augmentation en pourcentage : [(Prix final – Prix initial) / Prix initial] x 100. Elle permet de calculer l’augmentation en pourcentage d’un produit.

Application SOFGYM

Énoncé :

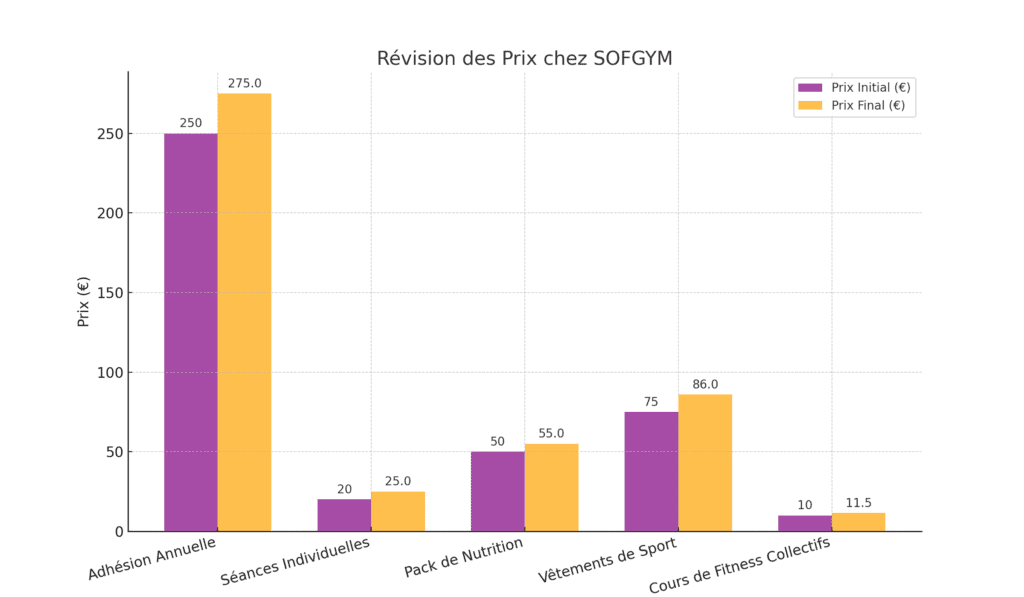
La société SOFGYM, spécialisée dans l’industrie du sport et du bien-être, a décidé de revoir ses prix suite à une restructuration interne et une augmentation des coûts de production.

1. Le prix d’adhésion annuelle est actuellement de 250 €. SOFGYM compte augmenter ce prix de 10%. Quel sera le nouveau prix?

2. Le prix des séances individuelles passe de 20 € à 25 €. Quel est le pourcentage de l’augmentation?

3. Un pack de nutrition autrefois vendu à 50 € coûtera désormais 55 €. Quel est le taux d’augmentation?

4. SOFGYM a revu les prix de ses vêtements de sport. Un ensemble qui coûtait autrefois 75 € coûte désormais 86 €. Quelle est l’augmentation en pourcentage?

5. L’entreprise envisage d’augmenter le prix de ses cours de fitness collectifs de 15%. Si le prix actuel est de 10 €, quel sera le nouveau prix?

Travail à faire :

1. Calculez le nouveau prix d’adhésion annuelle après l’augmentation.
2. Calculez le pourcentage de l’augmentation du prix des séances individuelles.
3. Calculez le taux d’augmentation du pack de nutrition.
4. Calculez l’augmentation en pourcentage du prix des vêtements de sport.
5. Calculez le nouveau prix des cours de fitness collectifs après l’augmentation.

Proposition de correction :

1. Le nouveau prix d’adhésion annuelle est : 250 € + (250 € * 10 / 100) = 250 € + 25 € = 275 €.
2. Le pourcentage d’augmentation des séances individuelles est : ((25 € – 20 €) ÷ 20 €) * 100 = 25%.
3. Le taux d’augmentation du pack de nutrition est : ((55 € – 50 €) ÷ 50 €) * 100 = 10%.
4. L’augmentation en pourcentage des prix de vêtements de sport est : ((86 € – 75 €) ÷ 75 €) * 100 = 14,67% (arrondi au centième de près).
5. Le nouveau prix des cours de fitness collectifs sera : 10 € + (10 € * 15% ÷ 100) = 10 € + 1,5 € = 11,5 €.

Récapitulatif des Formules Utilisées :

– Nouveau prix après augmentation : Prix actuel + (Prix actuel * Taux d’augmentation ÷ 100)
– Pourcentage d’augmentation : ((Nouveau prix – Ancien prix) ÷ Ancien prix) * 100

Application Delicious Breads

Énoncé :

Pierre est le propriétaire de l’entreprise « Delicious Breads », une boulangerie réputée en ville. Il a récemment réalisé une augmentation sur certains de ses produits.

1. Pierre a augmenté le prix du pain baguette de 1,00 € à 1,20 €.
2. Le prix de la brioche, qui était à l’origine de 1,50 €, a été augmenté à 1,80 €.
3. L’éclair au chocolat, autrefois vendu à 2,00 €, est maintenant à 2,40 €.
4. Le pain aux raisins, qui coûtait 1,10 €, est passé à 1,40 €.
5. Enfin, le croissant, précédemment à 0,90 €, est maintenant vendu à 1,10 €.

Travail à faire :

1. Quel est le pourcentage d’augmentation du prix du pain baguette ?
2. Quel est le pourcentage d’augmentation du prix de la brioche ?
3. Quel est le pourcentage d’augmentation du prix de l’éclair au chocolat ?
4. Quel est le pourcentage d’augmentation du prix du pain aux raisins ?
5. Quel est le pourcentage d’augmentation du prix du croissant ?

Proposition de correction :

1. Le pourcentage d’augmentation du prix du pain baguette est calculé comme suit : ((1,20 € – 1,00 €) ÷ 1,00 €) x 100 = 20 %

2. Le pourcentage d’augmentation du prix de la brioche est calculé de cette manière : ((1,80 € – 1,50 €) ÷ 1,50 €) x 100 = 20 %

3. Pour l’éclair au chocolat, le pourcentage d’augmentation est : ((2,40 € – 2,00 €) ÷ 2,00 €) x 100 = 20 %

4. Le pourcentage d’augmentation du prix du pain aux raisins est : ((1,40 € – 1,10 €) ÷ 1,10 €) x 100 = 27,27 % (arrondi au deuxième chiffre après la virgule pour obtenir un pourcentage précis)

5. Pour le croissant, le pourcentage d’augmentation est calculé comme suit : ((1,10 € – 0,90 €) ÷ 0,90 €) x 100 = 22,22 % (arrondi au deuxième chiffre après la virgule pour obtenir un pourcentage précis)

Récapitulatif des Formules Utilisées :

– Pourcentage d’augmentation = ((Nouveau montant – Ancien montant) ÷ Ancien montant) x 100
Cette formule est utilisée pour calculer le pourcentage d’une augmentation. Elle permet de déterminer de combien un certain montant a été augmenté en termes de pourcentage.
Note : Les résultats pour les questions 4 et 5 sont arrondis au deuxième chiffre après la virgule pour plus de précision.

Application Fruits d’été

Énoncé :

Faisons l’étude de l’entreprise « Fruits d’été », une start-up qui produit et vend une variété de jus de fruits. Au premier semestre 2021, le prix de vente (HT) d’un litre de jus était de 10 €. L’entreprise a récemment augmenté ses prix pour tenir compte de l’inflation et des augmentations des coûts des matières premières. Les nouveaux prix sont désormais de 12 € le litre (HT).

Travail à faire :

1. Calculez l’augmentation en euros.
2. Calculez l’augmentation en pourcentage du prix initial.
3. Si l’entreprise a vendu 1000 litres de jus au premier semestre à l’ancien prix, quel serait le revenu supplémentaire généré avec le nouveau prix, en supposant que le volume de ventes reste le même ?
4. Si la TVA en vigueur est de 20 %, calculez le nouveau prix de vente TTC.
5. Supposons que le taux d’inflation de cette année soit révisé à 10 %. Fruits d’été devra-t-il réajuster ses prix ? Si oui, quel sera le nouveau prix ?

Proposition de correction :

1. L’augmentation en euros est le nouveau prix de vente (12 €) moins l’ancien prix de vente (10 €), soit 12 € – 10 € = 2 €.

2. L’augmentation en pourcentage est connue en appliquant la formule d’augmentation ÷ prix initial x 100. Cela donne donc (2 € ÷ 10 €) x 100 = 20%.

3. Si l’entreprise avait vendu 1000 litres de jus au nouveau prix, le revenu supplémentaire serait: (Prix de vente nouveau – Prix de vente ancien) x quantité vendue = (12 € – 10 €) x 1000 = 2000 €.

4. On peut calculer le nouveau prix de vente TTC en ajoutant la TVA au prix HT. Donc, le nouveau prix TTC = prix HT (nouveau) + (prix HT (nouveau) x TVA/100). Cela donne donc 12 € + (12 € x 20 / 100) = 12 € + 2,4 € = 14,4 €.

5. Si l’inflation est revue à 10%, la nouvelle augmentation nécessitée serait donc de 10 € x 10% = 1 €. Donc, le nouveau prix de vente serait 10 € + 1 € = 11 €. Mais comme ils ont déjà augmenté le prix à 12 €, ils n’ont pas besoin de réajuster leurs prix.

Récapitulatif des Formules Utilisées :

1. Augmentation en euros = Prix de vente nouveau – Prix de vente ancien
2. Augmentation en pourcentage = (Augmentation en euros ÷ Prix de vente ancien) x 100
3. Revenu supplémentaire = (Prix de vente nouveau – Prix de vente ancien) x Quantité vendue
4. Prix de vente TTC = prix HT (nouveau) + (prix HT (nouveau) x TVA/100)
5. Nouveau prix en cas d’inflation = Prix de vente ancien + (Prix de vente ancien x Taux d’inflation / 100)