Tableau d’emprunt – Annuité – Trimestrialité : 13 Exercices corrigés

Bienvenue dans cet article dont l’unique but est de vous aider à progresser sur le chapitre intitulé le financement des investissements à l’aide d’exercices corrigés de la matière Gestion Opérationnelle du BTS MCO.

Cette thématique d’exercices corrigés Tableau d’emprunt a été créé pour maitriser tous les éventualités de calculs du financement des investissements.

Si vous souhaitez dans un premier temps voir ou revoir le cours sur le financement des investissements, je vous invite à lire mon article

Les 7 exercices corrigés sur le tableau d’emprunt de cette page portent principalement sur le tableau d’emprunt et l’annuité constante.

Vous trouverez également des exercices corrigés sur les notions suivantes : le calcul de l’annuité constante, le calcul d’annuités constantes trimestrielles le calcul d’annuités constantes semestrielles et mensuelles.

Voici la liste des 13 exercices corrigés sur le tableau d’emprunt :

1. Exercice N°1 : Tableau d’emprunt emprunt – Remboursement par amortissements constants
2. Exercice N°2 : Tableau d’emprunt – Remboursement par annuités constantes
3. Exercice N°3 : Calcul de taux mensuel proportionnel proportionnel
4. Exercice N°4 : Calcul de la semestrialité d’un emprunt
5. Exercice N°5 : tableau d’emprunt – Remboursement par amortissements constants
6. Exercice N°6 : Tableau d’amortissement – Remboursement par annuités constantes
7. Exercice N° 7 : Calcul de l’annuité constante
8. Exercice N°8 : Calcul d’une mensualité constante
9. Exercice N°9 : Calcul d’une trimestrialité constante
10. Exercice N°10 : Calcul d’une semestrialité constante
11. Exercice N°11 : Extrait Tableau d’amortissement
12. Exercice N°12 : Extrait Tableau d’emprunt – Semestrialités constantes
13. Exercice N°13 : Extrait Tableau d’emprunt – Trimestrialités constantes

Exercices corrigés Tableau d’emprunt N°1 : Remboursement par amortissements constants

Énoncé

L’unité commerciale Ide fabrique et vend des déguisements pour tout public : petits, grands, particuliers et professionnels.

M Lecas, le responsable de l’unité commerciale souhaite investir dans un nouveau local d’un montant de 365 000 €.

Pour cette raison, il vous remet des éléments concernant le mode de financement pour apporter des réponses à ses questions.

Mode de financement :

• Type de financement : Emprunt ;
• Taux d’intérêt : 6 % l’an ;
• Montant emprunté : Montant du local ;
• Durée de remboursement : 4 ans.
• Type de remboursement : Amortissements constants

Travail à faire

1. Présentez le plan d’amortissement de l’emprunt.

Exercice corrigé N°1

(1) : Capital restant dû début de période multiplié par le taux d’intérêt

donc : 365 000 × 0,06

(2) : il s’agit d’un mode de remboursement par amortissement constant donc vous devez diviser le montant de l’emprunt par le nombre de périodes

donc : 365 000 ÷ 4

(3) : le calcul de l’annuité est égal à la somme de l’intérêt et de l’amortissement

donc : Intérêts + Amortissement pour chaque ligne soit 21 900 + 91 250

(4) : le capital restant dû fin de période prend en compte uniquement les montants d’amortissement de la ligne

donc : capital restant dû début de période – Amortissement soit 365 000 – 91 250

Exercices corrigés Tableau d’emprunt N°2 : Remboursement par annuités constantes

Énoncé

L’unité commerciale Lepin est spécialisée dans la fabrication de pains, et de gâteaux.

Ses produits sont destinés aussi bien aux particuliers qu’aux professionnels.

L’entreprise souhaite investir dans un nouveau four, pour un montant de 150 000 € HT, mais hésite sur le mode de financement.

Son responsable M Lalevure vous communique certains éléments relatifs au mode de financement.

Mode de financement :

• Type de financement : Emprunt ;
• Taux d’intérêt : 4,5 % l’an ;
• Montant emprunté : Montant de l’investissement ;
• Durée de remboursement : 5 ans.
• Type de remboursement : Annuités constantes

Travail à faire

1. Présentez le plan d’amortissement de l’emprunt.

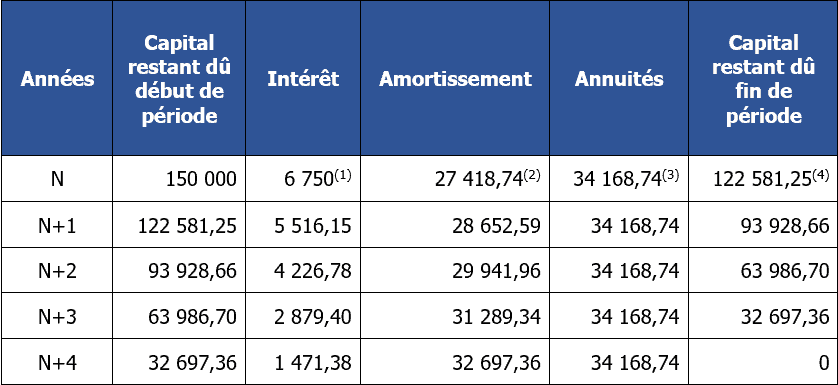
Exercice corrigé N°2

Tout d’abord il est nécessaire de calculer le montant de l’annuité constante avant de réaliser le tableau demandé.

Pour cela nous allons appliquer la formule suivante :

a = V₀ × [i ÷ (1 – (1+i)^-n)]

Soit donc :

a = 150 000 × [0,045 ÷ (1 – (1 + 0,045)^-5)]

D’où a = 34 168,74 €

(1) : Pour calculer l’intérêt, vous devez multiplier le capital restant dû par le taux d’intérêt

donc : 150 000 × 0,045

(2) : Pour calculer le montant de l’amortissement, vous devez soustraire le montant de l’intérêt au montant de l’annuité constante

donc : (3) – (1) soit 34 168,74 – 6 750

(3) : Pour calculer l’Annuité constante, il faut appliquer la formule vu plus haut et recopier le résultat

(4) : le capital restant dû fin de période prend en compte uniquement les montants d’amortissement de la ligne

donc : capital restant dû début de période – Amortissement soit 150 000 – 27 418,74

Exercices corrigés Tableau d’emprunt N°3 : Calcul de taux mensuel proportionnel

Énoncé

L’unité commerciale Lesson souhaite emprunter un capital de 135 000 € afin de financer un projet d’investissement.

On vous transmet les conditions bancaires en annexe 1.

Annexe 1 : Conditions bancaires

Taux d’intérêt annuel : 5,75 %

Fréquence des remboursements : Mensuels

Travail à faire

1. Calculez le taux mensuel proportionnel.

Exercice corrigé N°3

Dans cet exercice il est nécessaire de calculer le taux mensuel proportionnel car la fréquence de remboursement et la périodicité du taux sont différentes.

Calcul du taux mensuel proportionnel :

Taux = 5,75 % / 12 soit 0,48 %

Le taux mensuel proportionnel est donc de 0,48 %.

Si l’on souhaite calculer le montant de la mensualité constante, il suffit d’appliquer la formule de l’annuité constante mais en tenant compte du taux mensuel proportionnel et d’un nombre de mois et non d’années.

Exercice N°4 : Calcul de la semestrialité d’un emprunt

Énoncé

L’unité commerciale Cayo est spécialisée dans la distribution de matériels médicaux pour les hôpitaux.

Elle souhaite investir dans une nouvelle technologie (125 000 € HT) mais hésite sur les conditions bancaires.

En effet, elle souhaite emprunter car le montant de l’investissement est très important.

L’entreprise souhaite rembourser la totalité du montant sur 5 ans.

Annexe 1 : Conditions bancaires

Taux d’intérêt annuel : 5,75 %

Fréquence des remboursements : Semestriel

Travail à faire

1. Calculez la semestrialité de l’emprunt.

Exercice corrigé N°4

Dans cet exercice il est nécessaire de calculer le taux semestriel proportionnel car la fréquence de remboursement et la périodicité du taux sont différentes.

Calcul du taux semestriel proportionnel :

Taux = 5,75 % ÷ 2 (2 semestres) soit 2,875 %

Le taux semestriel proportionnel est donc de 2,875 %.

Si l’on souhaite calculer le montant de la semestrialité constante, il suffit d’appliquer la formule de l’annuité constante mais en tenant compte du taux semestriel proportionnel et d’un nombre de semestres et non d’années.

Ainsi on a :

Calcul du nombre de semestres : 5 ans x 2 semestres = 10 semestres

On a donc :

125 000 × [0,02875 ÷ (1 – (1 + 0,02875)^-10] = 14 560,48 €

Le montant de la semestrialité est donc de 14 560,48 €.

Exercices corrigés Tableau d’emprunt N°5 : Amortissement constant

Énoncé

On donne les éléments suivants :

Montant de l’emprunt en N : 20 000 €

Taux annuel : 6,5 %

Type de remboursement : Amortissement constant

Durée de l’emprunt : 5 ans

Travail à faire

1. Présentez le tableau de remboursement de l’emprunt.

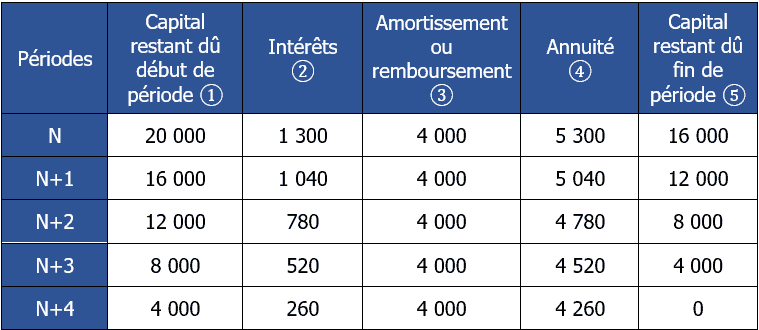
Exercice corrigé N°5

? : report de ?

? : ? x 0,065

? : 20 000 ÷ 5 ans

? : ? + ?

? : ? – ?

Exercices corrigés Tableau d’emprunt N°6 : Remboursement par annuités constantes

Énoncé

On donne les éléments suivants :

Montant de l’emprunt en N : 10 000 €

Taux annuel : 4,5 %

Type de remboursement : Annuités constantes

Durée de l’emprunt : 5 ans

Travail à faire

1. Présentez le tableau de remboursement de l’emprunt.

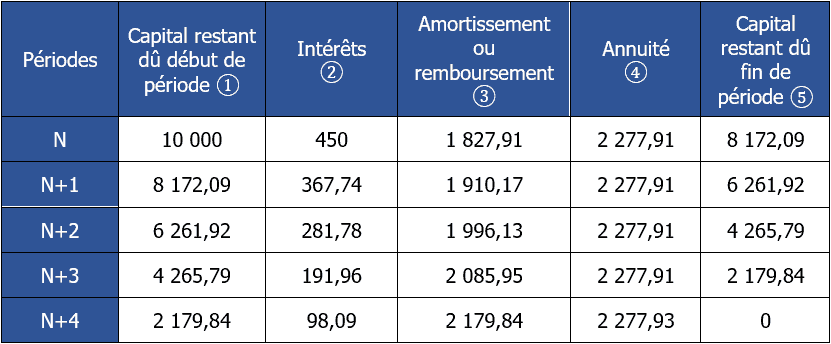
Exercice corrigé N°6

Dans un premier temps, il faut calculer le montant de l’annuité constante en appliquant la formule suivante :

Emprunt × [taux d’intérêt ÷ (1 – (1 + taux d’intérêt)^-n)]

Ainsi on a le calcul suivant :

10 000 × [0,045 ÷ (1 – (1 + 0,045)^-5)] = 2 277,91 €

On peut maintenant réaliser le tableau demandé :

? : report de ?

? : ? × 0,045

? : ? – ?

? : selon calcul de l’annuité constante

? : ? – ?

Exercices corrigés Tableau d’emprunt N°7 : Calcul d’une annuité constante

Énoncé

On donne les éléments suivants :

Montant de l’emprunt en N : 15 000 €

Taux annuel : 3,5 %

Type de remboursement : Annuités constantes

Durée de l’emprunt : 5 ans

Travail à faire

1. Calculez le montant de l’annuité constante.

Exercice corrigé N°7

Pour réaliser le travail demandé, nous allons utiliser la formule suivante :

Emprunt × [taux d’intérêt ÷ (1 – (1 + taux d’intérêt)^-n)]

Ainsi on a :

15 000 × [0,035 ÷ (1 – (1 + 0,035)^-5)] = 3 322,22 €

Le montant de l’annuité constante est donc de 3 322,22 €.

Exercices corrigés Tableau d’emprunt N°8 : Calcul d’une mensualité constante

Énoncé

On donne les éléments suivants :

Montant de l’emprunt en N : 35 000 €

Taux mensuel : 0,54 %

Type de remboursement : Mensualités constantes

Durée de l’emprunt : 5 ans

Travail à faire

1. Calculez le montant de l’annuité constante.

Exercice corrigé N°8

Dans cet exercice corrigé, le calcul ne pose pas de problème particulier.

Il faut juste adapter le nombre de périodes (5 ans x 12 mois = 60 mois) en prenant la formule de l’annuité constante suivante :

Emprunt × [taux d’intérêt ÷ (1 – (1 + taux d’intérêt)^-n)]

Ainsi on a le calcul suivant :

35 000 × [0,0054 ÷ (1 – (1 + 0,0054)^-60)] = 684,49 €

Le montant de la mensualité constante est donc de 684,49 €.

Exercices corrigés Tableau d’emprunt N°9 : Calcul d’une trimestrialité constante

Énoncé

On donne les éléments suivants :

Montant de l’emprunt en N : 65 000 €

Taux trimestriel : 0,65 %

Type de remboursement : Trimestrialités constantes

Durée de l’emprunt : 5 ans

Travail à faire

1. Calculez le montant de la trimestrialité constante.

Exercice corrigé N°9

Dans cet exercice corrigé, il faut faire attention à adapter la formule de l’annuité constante en fonction du nombre de mois.

En effet, il s’agit ici de trimestrialités constantes.

Dans cinq ans il y a 5 x 4 trimestres soit au total 20 trimestres.

La formule à adapter est la suivante :

Emprunt × [taux d’intérêt ÷ (1 – (1 + taux d’intérêt)^-n)]

Ainsi on a :

65 000 × [0,065 ÷ (1 – (1 + 0,065)^-20)] = 3 476,36 €

Le montant de la trimestrialité constante est donc de 3 476,36 €.

Exercices corrigés Tableau d’emprunt N°10 : Calcul d’une semestrialité constante

Énoncé

On donne les éléments suivants :

Montant de l’emprunt en N : 65 000 €

Taux semestriel : 0,65 %

Type de remboursement : Semestrialités constantes

Durée de l’emprunt : 5 ans

Travail à faire

1. Calculez le montant de la semestrialité constante.

Exercice corrigé N°10

Dans cet exercice, il faut adapter la formule de l’annuité constante car il s’agit ici de semestrialités et non d’annuités constantes.

Nous allons donc transformer la formule suivante en précisant un nombre de périodes égale à 5 ans x 2 semestres soit au total 10 semestres sur la période :

Emprunt × [taux d’intérêt ÷ (1 – (1 + taux d’intérêt)^-n)]

Ainsi on a le calcul suivant :

65 000 × [0,0065 ÷ (1 – (1 + 0,0065)^-10)] = 6 734,63 €

Le montant de la semestrialité constante est donc de 6 734,63 €.

Exercices corrigés Tableau d’emprunt N°11 : Extrait Tableau d’emprunt – Mensualités constantes

Énoncé

On donne les éléments suivants :

Montant de l’emprunt en N : 25 000 €

Taux mensuel : 1,5 %

Type de remboursement : Mensualités constantes

Durée de l’emprunt : 5 ans

Travail à faire

1. Présentez les 3 premières lignes du tableau de remboursement de l’emprunt.

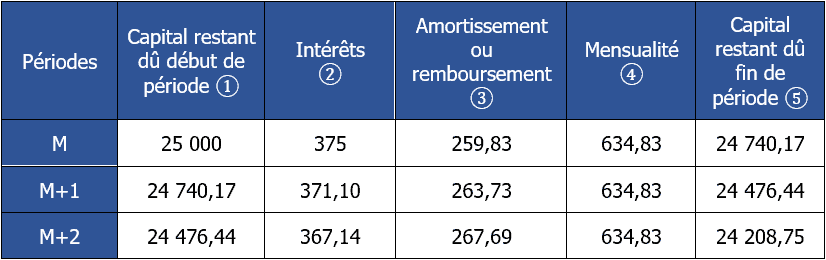
Exercice corrigé N°11

Dans un premier temps, il est nécessaire de calculer le montant de la mensualité constante en adaptant la formule suivante :

Emprunt × [taux d’intérêt ÷ (1 – (1 + taux d’intérêt)^-n)]

Ainsi on a :

25 000 × [0,015 ÷ (1 – (1 + 0,015)^-60)] = 634,83 €

Le montant de la mensualité constante est donc de 634,83 €.

? : report de ?

? : ? × 0,015

? : ? – ?

? : selon calcul de la mensualité constante

? : ? – ?

Exercices corrigés Tableau d’emprunt N°12 : Extrait Tableau d’emprunt – Semestrialités constantes

Énoncé

On donne les éléments suivants :

Montant de l’emprunt en N : 45 000 €

Taux semestriel : 1,75 %

Type de remboursement : Semestrialités constantes

Durée de l’emprunt : 6 ans

Travail à faire

1. Présentez les 3 premières lignes du tableau de remboursement de l’emprunt.

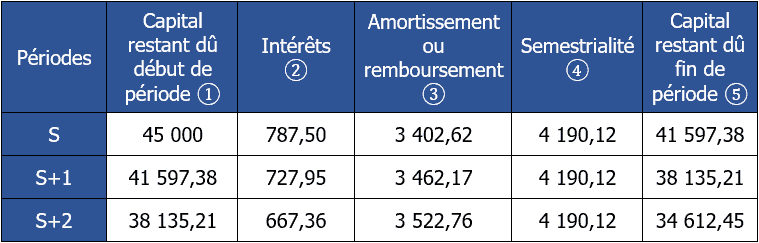
Exercice corrigé N°12

Dans un premier temps, il est nécessaire de calculer le montant de la semestrialité constante en adaptant la formule suivante :

Emprunt × [taux d’intérêt ÷ (1 – (1 + taux d’intérêt)^-n)]

Ainsi on a :

45 000 × [0,0175 ÷ (1 – (1 + 0,0175)^-12)] = 4 190,12 €

Le montant de la semestrialité constante est donc de 4 190,12 €.

? : report de ?

? : ? × 0,0175

? : ? – ?

? : selon calcul de la semestrialité constante

? : ? – ?

Exercices corrigés Tableau d’emprunt N°13 : Extrait Tableau d’emprunt – Trimestrialités constantes

Énoncé

On donne les éléments suivants :

Montant de l’emprunt en N : 45 000 €

Taux trimestriel : 2,95 %

Type de remboursement : Trimestrialités constantes

Durée de l’emprunt : 9 ans

Travail à faire

1. Présentez les 3 premières lignes du tableau de remboursement de l’emprunt.

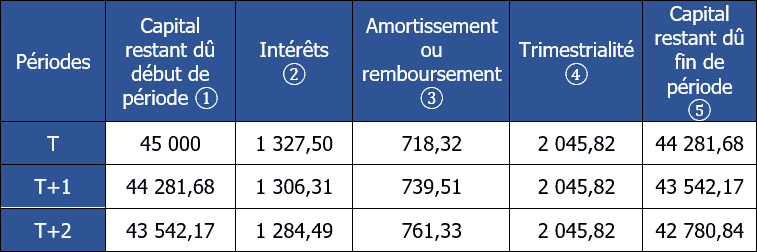
Exercice corrigé N°13

Dans un premier temps, il est nécessaire de calculer le montant de la trimestrialité constante en adaptant la formule suivante :

Emprunt × [taux d’intérêt ÷ (1 – (1 + taux d’intérêt)^-n)]

Ainsi on a :

Il y a 9 x 4 trimestres sur la période de 9 ans soit au total 36 trimestres.

45 000 × [0,0295 ÷ (1 – (1 + 0,0295)^-36)] = 2 045,82 €

Le montant de la trimestrialité constante est donc de 2 045,82 €.

? : report de ?

? : ? × 0,0295

? : ? – ?

? : selon calcul de la trimestrialité constante

? : ? – ?