Bienvenue dans cet article dont l’unique but est de vous aider à progresser sur le chapitre de la prévision des ventes à l’aide d’exercices corrigés de la matière Gestion Opérationnelle du BTS MCO.
Si vous souhaitez dans un premier temps voir ou revoir le cours sur la prévision des ventes, je vous invite à lire mon article Prévision des Ventes : Les 4 Méthodes à Maîtriser.
Les 6 exercices corrigés sur la prévision des ventes de cette page portent principalement sur le calcul de prévision des ventes.
Vous trouverez également des exercices corrigés sur les notions suivantes : la méthode des moindres carrés, la méthode des points extrêmes et la méthode de la double moyenne (Méthode de Mayer).
Voici la liste des 6 exercices de prévision des ventes exercices corrigés :
- Prévision des ventes Exercices corrigés : Chiffre d’affaires – Méthode des moindres carrés
- Prévision des ventes Exercices corrigés : Méthode des points extrêmes
- Prévision des ventes Exercices corrigés : Chiffre d’affaires prévisionnel – Méthode de la double moyenne
- Prévision des ventes Exercices corrigés : Chiffre d’affaires – Méthode des moindres carrés
- Prévision des ventes Exercices corrigés : Méthode des points extrêmes
- Prévision des ventes Exercices corrigés : Chiffre d’affaires – Méthode de Mayer
Prévision des ventes Exercices corrigés : Chiffre d’affaires – Méthode des moindres carrés
Énoncé
L’unité commerciale Mionneur fabrique et vend des pièces détachées pour des camions à destination des professionnels de la route.
Sa responsable, Madame Laroutière, souhaite effectuer une estimation de son chiffre d’affaires pour l’année N+1.
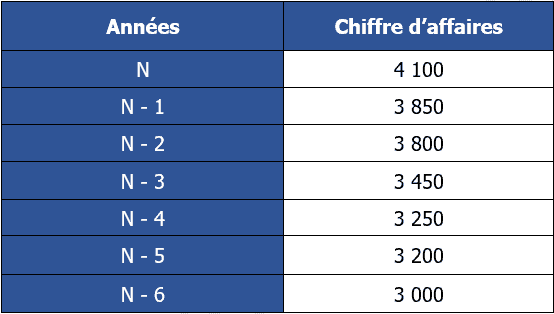
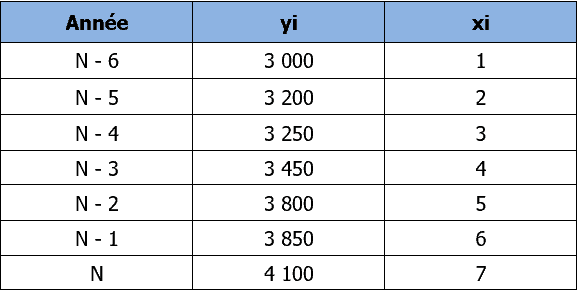
Pour cela, elle vous remet l’évolution de son chiffre d’affaires pour les sept années précédentes.
Travail à faire
- Déterminez le chiffre d’affaires prévisionnel N+1 selon la méthode des moindres carrés.
Proposition de correction
- Déterminez le chiffre d’affaires prévisionnel N+1 selon la méthode des moindres carrés.
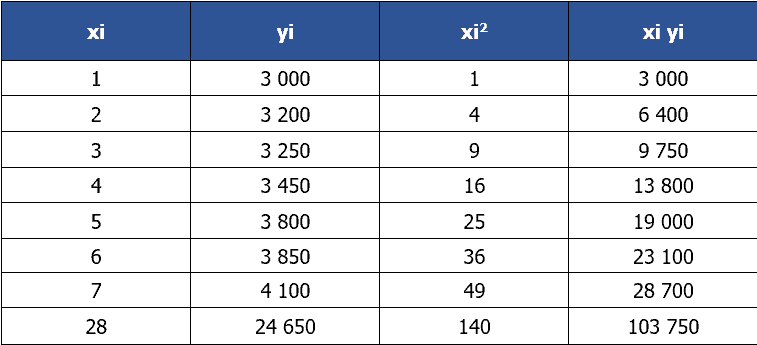
Afin de répondre à la question, il est nécessaire de réaliser un tableau préparatoire.
- xi correspond au rang de la période
- yi correspond aux chiffres d’affaires
- xi2 : 1 au carré, puis 2 au carré, puis 3 au carré et ainsi de suite.
- xi yi correspond au produit (à la multiplication) de xi et de yi soit donc : 1 × 3 000 puis 2 × 3 200, puis 3 × 3 250 et ainsi de suite.
- la dernière ligne est une ligne « Total ».
En créant ce tableau préparatoire, il est possible de trouver les éléments de l’équation dont nous avons besoin pour réaliser la prévision.
L’équation recherchée est de la forme :
Il faut donc calculer les éléments « a » et « b ».
Avant de calculer l’élément « a », il est nécessaire de calculer les moyennes de « x » et de « y ».
Pour calculer les moyennes, il faut utiliser les formules de gestion suivantes :
Ce qui donne dans notre exercice :
Avec « n » le nombre de variables dans notre tableau de base.
et
Ce qui donne dans notre exercice :
Maintenant que nous avons les moyennes de x (4) et de y (3 521,43), nous pouvons calculer l’élément « a » avec la formule suivante :
Nous avons tous les éléments chiffrés pour écrire la formule de l’élément « a » :
soit donc :
a = 183,93
en ce qui concerne « b », la formule est :
On admet que les moyennes vérifient l’équation, on remplace donc « x » et « y » par leur moyenne :
Ce qui donne avec les éléments chiffrés :
b = 3 521,43 – (183,93 × 4)
b = 2 785,71
Nous avons trouvé la valeur de « a » et la valeur de « b », nous pouvons donc maintenant écrire l’équation, de la forme y = ax + b, qui permet de calculer n’importe quel chiffre d’affaires prévisionnel :
y = 183,93x + 2 785,71
Calcul de la prévision
Nous pouvons finalement prévoir le chiffre d’affaires N+1, pour cela nous remplaçons « x » par le numéro de rang de l’année recherchée.
De N-6 à N, il y a 7 rangs, donc N+1 est le 8ième rang :
y = (183,93 × 8) + 2 785,71 = 4 257,15 €
Le chiffre d’affaires prévisionnel de l’unité commerciale est de 4 257,15 €.
Prévision des ventes Exercices corrigés : Méthodes des points extrêmes
Énoncé
L’unité commerciale Mouflet confectionne et vend des vêtements pour des professionnels du spectacle.
Sa responsable, Madame Lepatron, souhaite évaluer son chiffre d’affaires pour les deux années à venir.
Travail à faire
- Déterminez le chiffre d’affaires prévisionnel N+1 et N+2 selon la méthode des points extrêmes.
Proposition de correction
- Déterminez le chiffre d’affaires prévisionnel N+1 et N+2 selon la méthode des points extrêmes.
Afin de répondre à la question, il est nécessaire de réaliser un tableau préparatoire.
Dans cette méthode, seules la première et la dernière ligne sont à prendre en considération. On a donc deux points extrêmes :
x1 : 1 et y1 : 3 000 et x7 : 7 et y7 : 4 100
On pose le système d’équation à deux inconnues :
On peut résoudre ce système de plusieurs manières : par substitution ou par combinaison.
Ainsi nous pouvons faire la seconde équation moins la première :
4 100 – 3 000 = 7a + b – (1a + b)
1 100 = 7a + b – 1a – b
1 100 = 6a + 0b
Donc :
a = 1 100 / 6
a = 183,33
On peut maintenant retrouver « b » de la manière suivante :
b = y1 – ax1
On a donc :
b = 3 000 – (183,33 x 1)
b = 2 816,67
Calcul de la prévision
On peut maintenant faire les prévisions demandées à l’aide de l’équation suivante :
y = 183,33x + 2 816,67
Pour N+1 il faut remplacer « x » par le rang 8 car N avait le rang 7 :
y = (183,33 x 8) + 2 816,67
y = 4 283,31
Pour N+2 il faut remplacer « x » par le rang 9 ainsi on a :
y = (183,33 x 9) + 2 816,67
y = 4 466,64
Les chiffres d’affaires prévisionnels pour les années N+1 et N+2 sont donc de 4 283,31 € et de 4 466,64 €.
Prévision des ventes Exercices corrigés : Chiffre d’affaires prévisionnel – Méthode de la double moyenne
Énoncé
L’unité commerciale Nal fabrique et vend des tuyaux pour les communes et départements.
Ses clients ne réglant pas en temps et en heure, le responsable, M Leborgne, souhaite évaluer les futurs chiffres d’affaires.
Travail à faire
- Déterminez le chiffre d’affaires prévisionnel N+1 et N+2 selon la méthode de la double moyenne.
Proposition de correction
- Déterminez le chiffre d’affaires prévisionnel N+1 et N+2 selon la méthode de la double moyenne.
Cette méthode consiste à scinder la série statistique en deux sous séries puis à calculer les moyennes et finalement à résoudre un système d’équations dans lesquelles et sont les inconnues.
On peut ainsi scinder la série entre N-4 et N-3 :
Sous série 1 :
Calcul des moyennes de « x » et de « y »
et
D’où la première équation suivante :
Seconde sous série :
Calcul des moyennes de « x » et de « y »
et
D’où la seconde équation suivante :
On résout ensuite le système d’équations suivant :
On a donc :
3 560 – 3 075 = 6,5a – 2,5a +b – b
485 = 4a
a = 485 ÷ a = 121,25
On remplace ensuite « a » par sa valeur dans une des deux équations :
3 560 = 6,5a + b par exemple
Ce qui donne :
3 560 = 6,5 × 121,25 + b
3 560 = 788,12 + b
b = 3 560 – 788,12
b = 2 771,88
On obtient donc l’équation suivante :
Calcul de la prévision des ventes
Cette équation permet de trouver les chiffres d’affaires prévisionnels en remplaçant par le rang de l’année concernée.
Ici N+1(rang 9) nous donne :
y = (121,25 ×9) + 2 771,88
y = 3 863,13
Le chiffre d’affaires prévisionnel pour l’année N+1 est de 3 863,13 €.
Prévision des ventes Exercices corrigés : Chiffre d’affaires – Méthode des moindres carrés
Énoncé
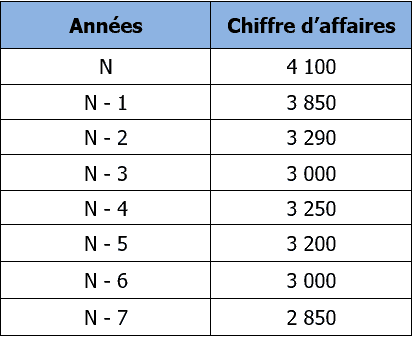
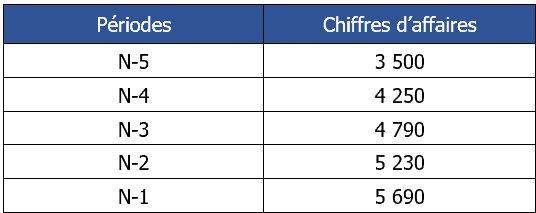
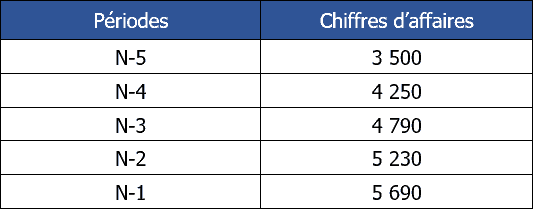
On donne le tableau suivant :
Travail à faire
- Déterminez le chiffre d’affaires prévisionnel N à l’aide de la méthode des moindres carrés.
Proposition de correction
Dans le thème de la prévision des ventes, « xi » représente le temps et « yi » les chiffres d’affaires.
Ainsi nous pourrons utiliser les formules suivantes :
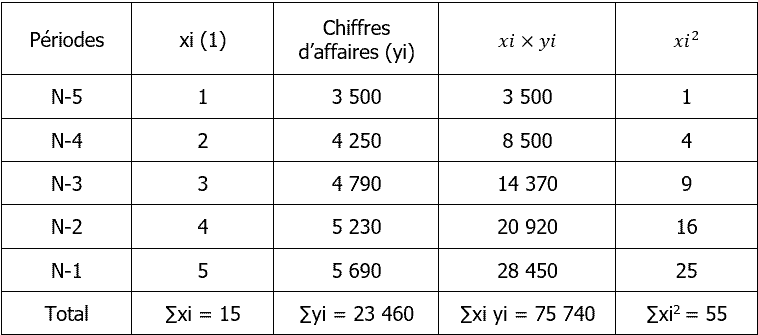
Nous allons maintenant concevoir un tableau préparatoire afin d’obtenir les éléments nécessaires à l’application des formules :
- une date ne peut pas être utiliser dans les formules. Il est donc nécessaire d’attribuer un numéro de rang, en partant de la date la plus ancienne, à chaque période.
On peut maintenant réaliser les calculs :
Calcul des moyennes :
Calcul de l’élément « a » :
Calcul de l’élément « b » :
b = 4 692 – (536 × 3) = 3 084
On peut donc écrire l’équation de la forme qui permet de trouver n’importe quels chiffres d’affaires :
y = 536x + 3 084
Calcul de la prévision des ventes
En remplaçant x par le numéro de rang correspondant à la période recherchée on a :
y = 536x + 3 084
y = (536 × 9) + 3 084
y = 6 300
Le chiffre d’affaires prévisionnel pour l’année N est de 6 300 €.
Prévision des ventes Exercices corrigés : Chiffre d’affaires – Méthode des points extrêmes
Énoncé
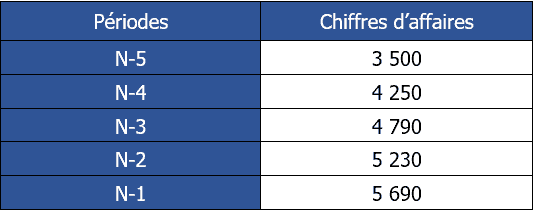
On donne le tableau suivant :
Travail à faire
- Déterminez le chiffre d’affaires prévisionnel N à l’aide de la méthode des points extrêmes.
Proposition de correction
Dans cet exercice de gestion corrigé, il est nécessaire dans un premier temps de déterminer les points extrêmes qui correspondent à la période la plus ancienne et à la période la plus récente.
Bien entendu, « xi » correspond aux périodes en indiquant un rang pour chacun d’entre eux et « yi » correspond aux chiffres d’affaires.
Ainsi, le tableau préparatoire peut être le suivant :
Points extrêmes :
P1 à pour coordonnées x1 = 1 et y1 = 3 500
P2 à pour coordonnées x2 = 5 et y2 = 5 690
Ensuite, on pose un système d’équations avec les paramètres « a » et « b » à déterminer qui permettra de trouver une équation de la forme « y = ax + b ».
Celle-ci nous permettra de trouver n’importe quel chiffre d’affaires futur.
Système d’équations :
Résolution du système d’équations par la méthode soustractive :
Nous allons faire la seconde équation moins la première.
5 690 – 3 500 = 5a – a + b – b
2 190 = 4a
a = 2 190 ÷ 4
a = 547,50
On trouve donc « a » = 547,50 et en remplaçant cette valeur dans l’une des équations de départ on peut trouver l’élément « b » :
3 500 = a + b
3 500 = 547,50 + b
b = 3 500 – 547,50
b = 2 952,50
Ainsi on trouve les éléments « a » et « b ». On peut maintenant écrire l’équation qui permet de trouver n’importe quel chiffre d’affaires futur :
y = 547,50x + 2 952,50
Calcul de la prévision des ventes
Pour trouver le chiffre d’affaires prévisionnel N, il faut remplacer par le rang correspondant à la période N : c’est donc le rang 6.
y = (547,50 × 6 ) + 2 952,50
y = 6 237,50
Ainsi le chiffre d’affaires prévisionnel N s’élève à 6 237,50 €.
Prévision des ventes Exercices corrigés : Chiffre d’affaires – Méthode de Mayer
Énoncé
On donne le tableau suivant :
Travail à faire
- Déterminez le chiffre d’affaires prévisionnel N à l’aide de la méthode de Mayer.
Proposition de correction
Dans cet exercice corrigé sur la prévision des ventes, il faut dans un premier temps partager la série statistique en deux sous séries, puis déterminer les moyennes pour x et y, en déduire une équation de la forme y = ax+b puis finalement résoudre un système d’équations en trouvant les paramètres « a » et « b ».
Première sous-série :
Calcul des moyennes :
D’où l’équation suivante :
Seconde sous-série :
Calcul des moyennes :
D’où l’équation suivante :
Ainsi on doit résoudre le système d’équations suivant :
Résolution du système d’équations par la méthode soustractive :
5 460 – 4 180 = 4,5a – 2a + – b
1 280 = 2,5a
a = 1 280 ÷ 2,5
a = 512
Pour trouver « b », il suffit de remplacer dans l’une des deux équations de base « a » par la valeur trouvée.
4 180 = (2 × 512) + b
4 180 = 1 024 + b
b = 4 180 – 1 024
b = 3 156
Ainsi on peut écrire l’équation qui permet de trouver n’importe quel chiffre d’affaires futur :
y = 512x + 3 156
Calcul de la prévision des ventes
Pour trouver la prévision demandée, il faut remplacer par le rang de la période demandée soit le rang 6 :
y = (512 × 6) + 3 156
y = 6 228
Donc le chiffre d’affaires prévisionnel N est de 6 228 €.
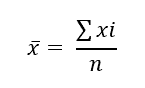
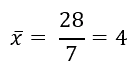
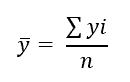
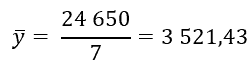
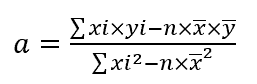
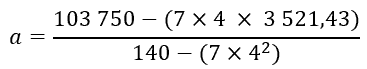
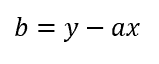
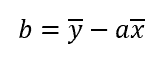
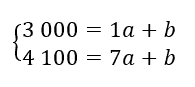
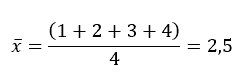
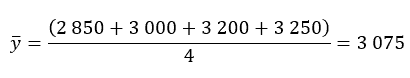
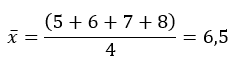
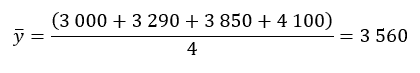
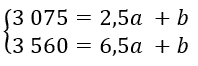
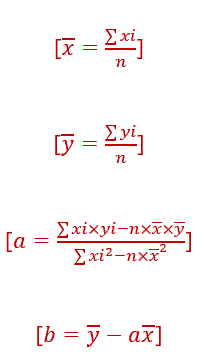
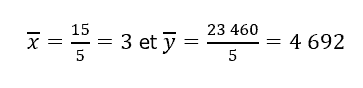
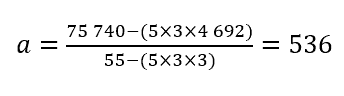

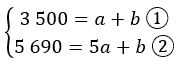

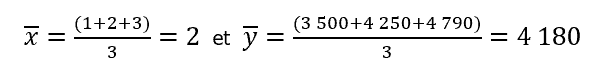

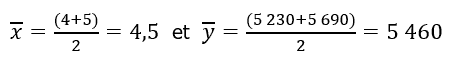
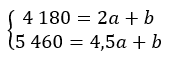
Super, merci beaucoup! Je suis en BTS PIM et vos exercices ont facilité l’ancrage et le contrôle des connaissances.
Je vous remercie pour votre commentaire Milvia. Je ne savais pas que la Gestion commerciale faisait partie du programme du BTS PI.
Je vous remercier
Je vous en prie. Profitez bien 🙂
Merci beaucoup. Egalement en BTS PI et vos exercices m’ont vraiment énormément aidé.
Bonjour !
Je suis content que cela puisse servir également à d’autres filières que le BTS MCO.
Bon courage à vous.
Bonjour n auriez vous pas des tableaux ou l’on rentrerais nos chiffre et le calcul se ferais ?
Bonjour Abellard,
Non je n’ai pas ces tableaux.
Bon courage à vous.
Bonjour,
s’il vous plaît est-ce que vous pouvez me laisser votre mail afin que je puisse vous contactez.
Merci d’avance
Bonjour et Bonne année 2023 à vous !
De quoi s’agit-il svp ?
Cordialement.
Merci pour votre appuie a notre égard veuillez nous donner en version pdf
Vous êtes le meilleur , Merci beaucoup
Bonjour,
Je vous remercie pour ce compliment.
Bon courage à vous.
bonjour
pourquoi dans le corrigé de l’exercice 1, le N-6 est égale a 4100 tandis que dans l’énoncé il est égale a 3000 et ce pour toutes les années
merci
Bonjour durand,
Voici le principe que vous devez comprendre : le rang 1 correspond à la période la plus lointaine. Il faut ensuite ajouter 1 à chaque fois.
Ainsi dans l’énoncé de l’exercice, l’année N-6 est la période la plus lointaine donc correspond au rang 1. Ensuite , N-5 correspond au rang 2 et ainsi de suite.
Les rangs correspondent à la colonne xi.
Autre rappel, l’année en-cours correspond à l’année N, il y a deux ans correspond à N-2, dans trois ans correspond à N+3.
Bon courage à vous.
merci beaucoup
Je vous en prie : Profitez !
Merci j’ai très bien compris le cours et j’ai réussi a faire les exercices sans regardé le corrigé en avance